HET_observability_constraints_with_astroplan.ipynb

{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Hobby-Eberly Telescope Observability Constraints with `astroplan`\n",
    "\n",
    "Michael Gully-Santiago  \n",
    "Research Fellow, UT Austin Astronomy  \n",
    "Sept. 25, 2020\n",
    "\n",
    "The [HET's fixed elevation design](https://en.wikipedia.org/wiki/Hobby%E2%80%93Eberly_Telescope) significantly constrains which observations are observable at any given time.  For example, an object may be observable for about an hour while it rises from the East, goes out of view because the telescope cannot steer to higher elevations, and then is visible again when it sets in the West.  \n",
    "\n",
    "The [HET provides a website](https://het.as.utexas.edu/HET/hetweb/ProgramPrep/hetdexcalendar.html) that can report these observability windows in PDF form.  But what if you have a large number of candidate targets for which you would like to assess observability?  In particular, what if you study ephemeral phenomena that must align with narrow time windows, such as exoplanet transits for atmospheric transmission spectroscopy?  In this case, a programmatic interface would be tremendously useful for winnowing the targets.\n",
    "\n",
    "In this notebook I adapt the [HET Observability](https://github.com/sjanowiecki/HET_observability) tool to use `astroplan`, an astropy-affiliated package for managing astronomical constraints.  The combination of these tools enables uses to combine multiple constraints to plan the best possible observations."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {},
   "outputs": [],
   "source": [
    "from astroplan import download_IERS_A\n",
    "download_IERS_A()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 2,
   "metadata": {},
   "outputs": [],
   "source": [
    "import astroplan\n",
    "from astroplan import Observer\n",
    "from astroplan import FixedTarget\n",
    "from astroplan import observability_table\n",
    "from astropy.time import Time\n",
    "\n",
    "from astropy.coordinates import SkyCoord\n",
    "\n",
    "import pandas as pd\n",
    "import astropy.units as u\n",
    "from os import listdir\n",
    "\n",
    "import numpy as np\n",
    "import matplotlib.pyplot as plt\n",
    "%matplotlib inline\n",
    "%config InlineBackend.figure_format = 'retina'"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Target list\n",
    "\n",
    "Let's begin with a target list.  These are fixed celestial targets."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {},
   "outputs": [],
   "source": [
    "names = ['Sirius', 'Castor', 'Pollux', 'Aldebaran', 'Polaris', 'Betelgeuse', 'Alpheratz', 'Merak', 'Mizar']"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "metadata": {},
   "outputs": [],
   "source": [
    "targets = [FixedTarget(coord=SkyCoord.from_name(name), name=name) for name in names]"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 5,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[<FixedTarget \"Sirius\" at SkyCoord (ICRS): (ra, dec) in deg (101.28715533, -16.71611586)>,\n",
       " <FixedTarget \"Castor\" at SkyCoord (ICRS): (ra, dec) in deg (113.64947164, 31.88828222)>,\n",
       " <FixedTarget \"Pollux\" at SkyCoord (ICRS): (ra, dec) in deg (116.32895777, 28.02619889)>,\n",
       " <FixedTarget \"Aldebaran\" at SkyCoord (ICRS): (ra, dec) in deg (68.98016279, 16.50930235)>,\n",
       " <FixedTarget \"Polaris\" at SkyCoord (ICRS): (ra, dec) in deg (37.95456067, 89.26410897)>,\n",
       " <FixedTarget \"Betelgeuse\" at SkyCoord (ICRS): (ra, dec) in deg (88.79293899, 7.407064)>,\n",
       " <FixedTarget \"Alpheratz\" at SkyCoord (ICRS): (ra, dec) in deg (2.09691619, 29.09043112)>,\n",
       " <FixedTarget \"Merak\" at SkyCoord (ICRS): (ra, dec) in deg (165.4603189, 56.38242609)>,\n",
       " <FixedTarget \"Mizar\" at SkyCoord (ICRS): (ra, dec) in deg (200.98141867, 54.92535197)>]"
      ]
     },
     "execution_count": 5,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "targets"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Observability\n",
    "\n",
    "Let's plan for a particular trimester: 2021-1\n",
    "\n",
    "> SUBJECT:  Call for HET and McDonald Observing Proposals (Trimester 2021-1)  \n",
    "> This trimester will cover the December 1 2020 to March 31 2021 period\n",
    "for HET and McDonald Proposals.  Read this call carefully.\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 6,
   "metadata": {},
   "outputs": [],
   "source": [
    "het = Observer.at_site('McDonald')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 7,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<Observer: name='McDonald',\n",
       "    location (lon, lat, el)=(-104.02166669444443 deg, 30.671666694444443 deg, 2074.9999999988677 m),\n",
       "    timezone=<UTC>>"
      ]
     },
     "execution_count": 7,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "het"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 8,
   "metadata": {},
   "outputs": [],
   "source": [
    "time_start = Time('2020-12-01 00:00:00') #start of Semester\n",
    "time_end = Time('2021-03-31 00:00:00') #end of Semester\n",
    "\n",
    "sunset_start = het.sun_set_time(time_start, which='next')\n",
    "sunrse_start = het.sun_rise_time(sunset_start, which='next')\n",
    "sunrse_end = het.sun_rise_time(time_end, which='next')\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 9,
   "metadata": {},
   "outputs": [],
   "source": [
    "time_range = (sunset_start, sunrse_end)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Set general observing constraints\n",
    "\n",
    "Observations should be at night, and at low airmass.  In practice, the HET observations will enforce low airmass by default anyways."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 10,
   "metadata": {},
   "outputs": [],
   "source": [
    "con1 = astroplan.AtNightConstraint().twilight_astronomical()\n",
    "con2 = astroplan.AirmassConstraint(2.5) # In practice the HET"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### HET-specific constraint "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "We will mimic this figure that shows the HET Observability constraint in terms of Declination and Hour Angle.\n",
    "\n",
    "![img](https://hydra.as.utexas.edu/imgs/ha_vs_dec.jpg)"
   ]
  },
  {
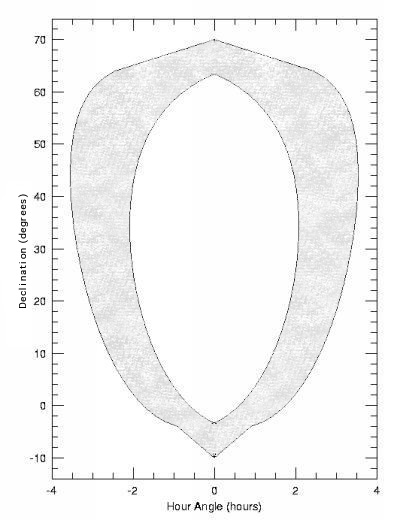   "cell_type": "code",
   "execution_count": 11,
   "metadata": {},
   "outputs": [],
   "source": [
    "tracking_file = 'https://raw.githubusercontent.com/sjanowiecki/HET_observability/master/data/HET_opt_tracking.txt'\n",
    "df_HET = pd.read_csv(tracking_file, names=['h_dec','h_tott','h_optaz','h_ha1','h_ha2'], delim_whitespace=True)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 12,
   "metadata": {},
   "outputs": [],
   "source": [
    "d2min = -4.318553207530732 \n",
    "d2max = 65.6814360000000\n",
    "df_HET['h_ha3'] = np.array([-h if ((d>d2min)&(d<d2max)) else 0 for h,d in zip(df_HET.h_ha2,df_HET.h_dec)])\n",
    "df_HET['h_ha4'] = np.array([-h if ((d>d2min)&(d<d2max)) else 0 for h,d in zip(df_HET.h_ha1,df_HET.h_dec)])"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 13,
   "metadata": {},
   "outputs": [],
   "source": [
    "df_HET['ha_max'] = df_HET[['h_ha1', 'h_ha2']].max(axis=1)\n",
    "df_HET['ha_min'] = df_HET[['h_ha1', 'h_ha2']].min(axis=1)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 14,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAjQAAAO+CAYAAAAT148JAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAWJQAAFiUBSVIk8AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nOzdd3hc5Z328e8zRZpRr7ZsIxeMGxiDMc0U00swkFBCyoYENpBN3g0h2SSLN2SzJGTJkiWhbAgpEGoIhBLTO8YGjDEuGAMuGPciW32kkaae5/1j5JGN5S7raGbuz3XNNXPOnDn6WZZG95ynGWstIiIiIpnM43YBIiIiIvtLgUZEREQyngKNiIiIZDwFGhEREcl4CjQiIiKS8RRoREREJOMp0IiIiEjGU6ARERGRjKdAIyIiIhlPgUZEREQyngKNiIiIZDwFGhEREcl4PrcLEDDGrAJKgNUulyIiItIXhgMha+2I3jqhAk3/UBIMBivGjRtX4XYhIiIiB9qSJUvo7Ozs1XMq0PQPq8eNG1cxf/58t+sQERE54CZNmsSCBQtW9+Y51YdGREREMp4CjYiIiGQ8BRoRERHJeAo0IiIikvEUaERERCTjKdCIiIhIxlOgERERkYyneWhERCRnOY5DU1MTbW1tRKNRrLVul5RxjDHk5+dTXFxMRUUFHo8710oUaEREJCc5jsO6devo6Ohwu5SMZq0lEokQiUQIh8PU1ta6EmoUaEREJCc1NTXR0dGBz+ejpqaGwsJC164uZDLHcQiHw9TV1dHR0UFTUxNVVVV9Xof+50REJCe1tbUBUFNTQ3FxscLMPvJ4PBQXF1NTUwN0f1/7vA5XvqqIiIjLotEoAIWFhS5Xkh22fh+3fl/7mgKNiIjkpK0dgHVlpncYYwBc61it/0URERHZb1sDjVsUaERERCTjKdCIiIhIxlOgERERkYynQCMiIiI8/vjjXHPNNZx88smUlJRgjOFrX/ua22XtMU2sJyIiIvzyl79k0aJFFBUVcdBBB7F06VK3S9orukIjIiIi3HrrrSxfvpxQKMRdd93ldjl7TVdoREREhNNOO83tEvaLrtCIiIhIxlOgERERkYynJicREZEeDJ/2nNsl7LHV/zPV7RJcpys0IiIikvEUaERERCTjqclJRESkB2rGySy6QiMiIiIZT4FGREREMp6anERERITp06czffp0AOrq6gB45513uOKKKwCoqqrilltucau83VKgEREREd5//33uv//+7fatXLmSlStXAjBs2LB+HWjU5CQiIiLccMMNWGt3elu9erXbJe6SAo2IiIhkPAUaERERyXgKNCIiIpLxFGhEREQk4ynQiIiISMZToBEREZGMp0AjIiIiGU+BRkRERDKeAo2IiIhkPAUaERERyXgKNCIiIpLxFGhEREQk4ynQiIiISMZToBEREZGMp0AjIiKS4xobG7n77ru56KKLOOSQQwgGg5SWlnLSSSdxzz334DiO2yXuls/tAkRERMRdjz32GN/5zncYNGgQp512GkOHDmXz5s08+eSTXHXVVbzwwgs89thjGGPcLnWnFGhERERy3OjRo3n66aeZOnUqHk93481NN93EscceyxNPPMGTTz7JJZdc4mKVu6YmJxERkRx3+umnc8EFF2wXZgBqamr49re/DcAbb7zhQmV7ToFGREREdsrv9wPg8/XvRh0FGhEREelRIpHggQceAODcc891uZpd699xS0RExC03lLpdwZ67ofWAnHbatGl8+OGHnHfeeZxzzjkH5Gv0Fl2hERERkR3ccccd/OY3v2Hs2LE8+OCDbpezWwo0IiIisp0777yTa6+9lkMPPZQZM2ZQUVHhdkm7pSYnERGRnhygZpz+7rbbbuMHP/gB48eP57XXXmPAgAFul7RHdIVGREREALj55pv5wQ9+wJFHHsmMGTMyJsyAAo2IiIgAN954I9OmTWPSpEm89tprVFVVuV3SXlGTk4iISI67//77+dnPfobX6+Xkk0/mjjvu2OGY4cOHc8UVV/R9cXtIgUZERCTHrVq1CoBkMsltt93W4zGnnHJKvw40anISERHJcTfccAPW2l3etPSBiIiIyAGmQCMiIiIZT4FGREREMp4CjYiIiGQ8BRoRERHJeAo0IiIikvEUaERERCTjKdCIiIhIxlOgERERkYynQCMiIiIZL2cDjTFmqjHmZWPMemNMpzFmpTHmMWPM5J0cf4Ix5nljTJMxpsMY84Ex5vvGGG9f1y4iIiLby8lAY4y5GXgWOAp4EbgdWAB8HnjbGPO1zxz/eWAWMAX4B3AnkAfcCjzSd5WLiIhIT3JutW1jTA3wI2AzMMFau2Wb504DXgd+ATzUta8E+DOQBE611s7r2v+fXcdeaoz5srVWwUZERMQluXiFZhipf/e724YZAGvtDKANqN5m96Vd249sDTNdx0aAn3ZtfueAViwiIiK7lIuB5hMgBhxrjKna9gljzBSgGHh1m92nd92/2MO5ZgEdwAnGmPwDUKuIiEifuO666zjjjDOora0lGAxSUVHBxIkT+fnPf05jY6Pb5e1WzjU5WWubjDHXAb8FPjbGTAcagZHAhcArwL9s85IxXffLezhXwhizCjgMOBhYsquvbYyZv5Onxu7VP0JERKSX3XrrrRx11FGcddZZDBgwgHA4zJw5c7jhhhv405/+xJw5c6itrXW7zJ3KuUADYK29zRizGvgLcPU2T60A7vtMU1Rp133rTk63dX9ZrxYpIiLSh0KhEIFAYIf9119/PTfddBO/+tWv+P3vf+9CZXsmF5ucMMb8O/A4cB+pKzOFwCRgJfBXY8yv9+Z0Xfd2dwdaayf1dAOW7tU/QEREpJf1FGYALrvsMgA++eSTvixnr+VcoDHGnArcDDxtrf03a+1Ka22HtXYBcBGwAfihMebgrpdsvQJTuuPZACj5zHEiIiJZ45lnngFgwoQJLleya7nY5HR+1/2Mzz5hre0wxswlFWwmkrpisww4GhgNbNcHxhjjA0YAia5jRUREMtott9xCe3s7ra2tzJs3j7feeosJEyYwbdo0t0vbpVwMNFtHI1Xv5Pmt+2Nd968D/wScC/ztM8dOAQqAWdbaaG8WKSIi7jr8/sPdLmGPLf7G4l471y233MLmzZvT2+eeey733Xcf1dU7+7PZP+RckxPwZtf9t4wxQ7Z9whjzOeBEIALM7tr9ONAAfNkYc/Q2xwaAX3Zt3nVAKxYREekjdXV1WGupq6vjySefZOXKlUycOJEFCxa4Xdou5WKgeZzUPDMDgSXGmPuNMTcbY54GniPVyXeatbYRwFobIjUSygu8YYy5u6vT8PvA5K7zPerCv0NEROSAGThwIBdddBEvv/wyjY2NfP3rX3e7pF3KuSYna61jjDkP+Ffgy6T6yxQATcDzwB3W2pc/85rpxphTgOuBS4AAqSHe/9Z1/G5HOImISGbpzWacTDZs2DAOPfRQ3n//fRoaGqiqqtr9i1yQc4EGwFobB27ruu3pa94GzjtgRYmIiPRTGzduBMDr9bpcyc7lYpOTiIiIbGPp0qXU1dXtsN9xHK6//nq2bNnCCSecQHl5uQvV7ZmcvEIjIiIi3V588UV+/OMfM2XKFEaOHEllZSWbN29m5syZrFy5kpqaGv785z+7XeYuKdCIiIjkuDPPPJNvfetbvP322yxatIiWlhYKCwsZPXo0l19+Od/73veoqKhwu8xdUqARERHJcePHj+fOO+90u4z9oj40IiIikvEUaERERCTjKdCIiIhIxlOgERERkYynQCMiIiIZT4FGREREMp4CjYiIiGQ8BRoRERHJeAo0IiIikvEUaERERCTjKdCIiIhIxlOgERERkYynQCMiIiIZT4FGREREMp4CjYiIiOzgwQcfxBiDMYa7777b7XJ2S4FGREREtrNu3TquueYaioqK3C5ljynQiIiISJq1liuvvJLKykq+/e1vu13OHlOgERERkbQ77riD119/nXvvvZfCwkK3y9ljCjQiIiICwJIlS5g2bRrXXnstU6ZMcbucvaJAIyIiIiQSCS6//HKGDh3KTTfd5HY5e83ndgEiIiL90ZKx49wuYY+NW7pkv8/xi1/8goULF/LWW28RDAZ7oaq+pSs0IiIiOW7u3LncdNNN/PCHP2Ty5Mlul7NPFGhERERy2NamptGjR3PjjTe6Xc4+U5OTiIhID3qjGScTtLe3s3z5cgACgUCPx1x99dVcffXVXHvttdx22219Wd4eU6ARERHJYfn5+Xzzm9/s8bkFCxawcOFCTjrpJMaMGdOvm6MUaERERHJYMBjc6dIGN9xwAwsXLuQb3/gGV111VR9XtnfUh0ZEREQyngKNiIiIZDwFGhEREenRDTfcgLW23zc3gQKNiIiIZAEFGhEREcl4CjQiIiKS8TRsW0QynuNYWjrjbGmLUN8Wpb4tSmN7jLZogrZInPZIgvZogo5YkoTjkEhaTlvwn4xcuhGA+OEBzps0CLw+8PjAXwCBEsjfeiuGwmooGgDFNVA0EILlYIzL/3IR2UqBRkQyQtKxrGvqYNnmNtY0hlnT2MHapg7WNXWwoaWTeNLu1fnObm3loM2p16we2gJrPt2r11tvHqZsKJQP775VjIQB46BsGHh0AVykLynQiEi/E0s4LNkUYuHaZj7cGGJZXRufbGkjEnd67WsY9i4A7fD6ZAwaV6Run2H9BZgB41LhZtCRcNAxMPAw8Pr362uKyM4p0IiI69oiceauauKdTxtZ0BViYom9Cy8+J0aeEyVAjAITI2ASBDyWfI9DwAv5HkueF3weg9cDMW8BEAbgk0gZocB5eGwCbBJfMkKejeB3Urc8p5MCG6bYdFBEByWeTgo88Z3WYuIdsGF+6rbwIQCsL4AZPDEVbkZMgaGTIb9on79nIv2Ntfv3IWF/KdCISJ9zHMvCdS3MWLqFtz9t4IP1rSSd3b8Z5iU7KXbaKfNEKPMnqMhzqAoYqgs8FOb7MNv1adna5OPt8Vw+X/fVkqjNo7Viwl79G7zJCAXRLQQjdRTG6ilONFLhNFBjmijxRnc43iQisPad1G32HViPD3PQMTDiFBh9NgyaqGaqPmaMwVqL4zh49L3fb1sDjXGpb5kCjYj0iUg8ydsrGnjl4828umQLDe07/tHfViDRTiUhBvoiDC5wGFLkoaIwr+vN0gPk9UndO5P0BmgrGEpbwdAdnstPtFHcsYbijrUMiK/jIDZR6Q1vd4xxEt0BZ+b/YItqMGPPgzFTU1dwfO7++3JBfn4+kUiEcDhMcXGx2+VkvHA49TOen5/vytdXoBGRA8ZxLHNXNzF94QaeW7yJtkii5wOtpSjRwiBPiKHBGAeXeqgqyu8KL+68Oe6PqK+YaMl4GkrGswp4FwgkQpS1L6e6YznDkqsZ7G3e7jWmvQ7m/QXm/QUbKMeMvxgmfAlqj9VoqgOkuLiYSCRCXV0dAIWFhRhjXLvCkImstVhrCYfD6e+jW+FQgUZEel1da4SH567lifnr2dDS2eMx/mSEQU49I4IRxpQbqoqDpN6SsvNtKeIroa7saOrKjmYxEEi2Uxn6iMEdHzHafkqhJ5Y+1kSaYd49MO8ebNlwzMSvwaRvpIaNS6+pqKggHA7T0dHB+vXr3S4nKxQUFFBRUeHK187Odw4R6XPWWt5Z2ciD76zh5Y8399gnJpBop5YGxhbHGVOVR57fBxT0fbH9QMRbxIby49hQfhzzbJKqjhUMCi1kTHIp5Z7u5inTshpm/BI782bMoRfCMVfD0ON11aYXeDweamtraWpqoq2tjWg06nrH1kxkjCE/P5/i4mIqKipc64+kQCMi+yXpWF78sI47Z6zg402hHZ73OVEOSm7m8JJOxlUHuzrjavjytqzxUl84hvrCMXxgHao7P2VY6xzGJpekR1MZJw4fPgEfPoEdfBRmyo9g9OfUkXg/eTweqqqqqKqqcrsU2U8KNCKyTxJJh38s3MBdb3zKyobwDs+Xx+oZH2hi0mA/BYF8QEOU94jxUF8wivqCUSy0cYaEFjC27W2GezZ1H7JxATzyVZyqMXim/BjGX6JgIzlPgUZE9oq1lleXbOHmF5eyYkv7ds95bILa+HqOLY9wyIgijFGI2R9J42dt6XGsLT2O8uh6DmmawXjnQ/wmNUePp2EZPHkVzlu34jn7FzDyDDVFSc5SoBGRPfbB+hZufPZj3lu9/QgdnxPjYGc9UwYmGVBagJqUel9z/kG8N+hyPkyGGNP0KhNi7xEwqVFjni0fwUOX4Aw/Gc/nbk7NSiySYxRoRGS3QpE4v3lpGQ/MWcO2fSa9TpxRyTWcOhgqioPuFZhDOr0lvF99MUuccxnT9CoTo++QvzXYrH4T+4eTYfK/Yk6dBnmFLlcr0ncUaERkl178cBM/e+ojtrR1T4RnrMOw+FrOqIkxsEx/NN0Q9RTwQdWFfJI8lQmNzzI+/j5eYzE2CbPvILn4cbwX3J6ahVgkByjQiEiP2iJxbnj6Y55YsP38HBWxzZxV3sTIgSWoacl9nd4S3h3wVZbFz+C4+kcZxjoAvG0b4eEv4ky6Es85/62rNZL1FGhEZAfz1zRx7SPvs765e1K8vGQnR3vXcNIhBfh8JS5WJz1p8Q/kpUHXMLJ9LseFnqXIRADwzL+X5Kdv4L3sXhg80eUqRQ4cjfMTkTRrLffPXs2X/jhnuzAzKLqeKweu59SDi/H5el7sUfoBY/i0+DieqJnGcu/Y9G5vyyqcu89Or/wtko0UaEQESC0e+cO/L+K/nv6IRNcsvz4nxmS7hG+MsVSW5OaMvpko6i3kjQH/zOsllxKxqWZBjxODp/6V5NPXQiK2mzOIZB41OYkILR0xvnn/POav6R6OXRxv4sLKLQyrUvNSRjKGFUXHsSUwktO33MMAGgDwLriPRMMKfF/9GwT0fyvZQ1doRHLchpZOLv3DO9uFmSHRtVw5tIVhVe6smiu9J+Sr4tma77PMPz69z7f2LeJ3nwNtm12sTKR3KdCI5LA1jWEuvWv2djP+jo8t5Z9GQVEw38XKpDclPPnMrPo67xaeld7nb/iYxJ/PgNYNLlYm0nsUaERy1LqmDr7653fZ1JoaDWOsw/HOx1wwpkgdf7ORMSwqPZs3Si7BsanlEXyhdcTvORdCm3bzYpH+T4FGJAdtau3kK3+ew4aW1Egmj01yqudjTj+kFKO1gLLa8qLjebni6yRs6u3fH1pL/J7PQXu9y5WJ7B8FGpEc0x5N8M/3zUsPy/bYJKd6lzJ5RLnLlUlfWRscz2sVl5PcGmpaVxF78FKId+7mlSL9lwKNSA5JJB2ueXgBSzaFgFQz08lmKccPL3O5Mulra4Ljeb3in9LNT3mb3yf292+C47hcmci+UaARySG/fmkZM5Z1Ny0clVzGiQcrzOSqVcEJvFN6QXo775PniM/4HxcrEtl3CjQiOeLVjzfzp1kr09uHxFZw1iFFLlYk/cFHRSezODg5ve1789c4n850sSKRfaNAI5IDNrZ08sPHFqW3K2N1fOFgHx6P3gIE5pR9ng2+4QAYLIm/X6FOwpJx9G4mkuWstfzHk4tp7YwDkJ/s4As1IfLytFK2pFjjZUbl1wiTWt4iL9pE55PXuFyVyN5RoBHJck8u2MDM5V2ftq3l1LxVDCwrdLco6Xc6vKXMrPhKeju48gUSHz7lYkUie0eBRiSLNYdj3Pjcx+nt4fHVHDW01MWKpD9bHxjL0uDR6W3nme9DtM3FikT2nAKNSBa7/bVPaOlINTUFkmGmHpTUxHmyS3NKL6DdpDqL50Wb6HhVo54kMyjQiGSplfXtPDRnTXr7GN9aSouCLlYkmSDmKeC90qnp7fx5f4TW9S5WJLJnFGhEstStr35CwrEAlMXqmVyrfjOyZz4JHsUW32AAvDZO+3M/c7kikd1ToBHJQqsawjz3wcb09snFDVpwUvac8TC39Pz0ZvCTpyC0cRcvEHGfAo1IFvrjzE/pujhDZWwzhw3SBHqydzbmHUKdfygAXpug7aVfuVyRyK4p0IhkmdaOOP9YuCG9fUxRkybQk71nDO8Xn5HeDCx9DGIdLhYksmt6lxPJMk8uXE80kVpgsCjezIQa9Z2RfbM2fxwt3koA/MlOwu895HJFIjunQCOSZR6Zuy79eKxffWdkPxjD0sLj05vJ9+51sRiRXVOgEckin2xuY9nm1ERoHpvgmAH6FZf9szx4NMmuPxUlLR/jNK/ZzStE3KF3O5Es8vziuvTjAYktlBcFXKxGskHEW8TG/EPS26F3/+piNSI7p0AjkkVe/rg70IwKhF2sRLLJqsCE9GOz9FkXKxHZOQUakSzR2B7lo40hAIx1mFClX2/pHWsCh6YfF7csgZjCsvQ/escTyRJzVjalH5cmmiktVHOT9I5ObzGNvhoAPDi0f/yKyxWJ7EiBRiRLvLuqMf14kFcrJEvv2rYfTWTpqy5WItIzBRqRLLF4Q2v68dBgwsVKJBttzhuefuzZvNi9QkR2QoFGJAskkg5LNoXS28NK9KstvavePyT9uCC0Aqx1sRqRHeldTyQLrG3qIBJPzQ6cl+ygsijP5Yok27R5K4mafAACyXaSrVqsUvoXBRqRLLCuuTP9uMjpwBjjYjWSlYwh5KtKb4Y3LHGxGJEdKdCIZIF1Td2LBhZ5Yi5WItmszVuRfhypW+ZiJSI7UqARyQLrmrsDTak37mIlks3avOXpx07TKhcrEdmRAo1IFqhvi6YfF/scFyuRbBb2lnVvtNXt/EARFyjQiGSB9kj3MO0Cn4uFSFaLebaZrDHa7l4hIj1QoBHJAuFYd6AJ+NQhWA6MeNcoJwAT1/IH0r8o0IhkgW2v0OR7XSxEslrMdF+h8SrQSD+jQCOSBZLbTHLm02+1HCCO2eaHy6qvlvQveusTyQJeT/evskVNTnJgeLYJMdboz4f0L/qJFMkCPk93iHGsAo0cGB4UaKT/0k+kSBbwbhNoEo7W2JEDw0Oye8NoOJ30Lwo0IlmgJOBPP+5M6gqNHBj5TvcEjgl/kYuViOxIgUYkC1QWdi9GGU4o0MiBEXC6RzYlA2W7OFKk7ynQiGSB8m0Dja7QyAGybaCxwUoXKxHZkQKNSBaoKuoONO0JTUQjB0ZBMpR+7CmqdrESkR0p0IhkgYPKC9KPQ07eLo4U2Xclicb0Y0/VSBcrEdmRAo1IFhhRVZh+3EZgF0eK7LvSZEP6cV7NOBcrEdmRxt2JZAAnFsNpb8dpayPZ3o7THsYm4qknLVQnkxy1ZSnHmSWc5nmfooUWBw+O8eDgwVoPceMjRh4x8oibPGL405Pw7bTXjd3JEPBtdpudPGF2N3p8m3Nvd47tzr37r7/7r217fJjc3Jx+7C2IsKrzpV18Iw6cA/Ul9+a8SRxiJknUkyRqksRMgphxcIyD0/U8Jsn71QX8e2OUIQnDB5Eq/J/Up8/h93ooyvdRHPBRHPBTlO8jT9NWSx9SoBFxkROJEN+wgdjatcQ3biRRX0+ioYFEfT3J+q771lZsLLbbc/33Z7a9XbetdN1m51qCcZ4tW+52Gf3eCoK8WRDklnWWf3lw0W6Pz/d5KC/Io7o4nwHF+dvdH1ReQG1FAbUVQfJ96vcl+0+BRqQPJJqaiC5fTnTZMiLLlxNfs5bYunUkNm92uzQB1mvAzl55xzN0j46LJhzqQhHqQpGdHmOAQaUBhlYWMLyykDE1xYytKWFsTfF2o/dEdkeBRqSXJZqb6Vz4Pp2LFhH58EMiy5eRrG/Y/Qt3wQGiPh9Rr5e4z0fM58Pxpj7VGmPApJpnKj0hKj3tPZ9kD9ogzJ60U+ymLSlifbQ5AeL2M80NOzm33ekxe1JwD+fYw1M4BhrzHVYMNsQrvRzR1L/bmzq9lk3BJG1+d2eCPmV9NTMaz2WArwmwWAuWVBNnHC8JfCSMn7jxwR4sj2CBja0RNrZGmLOyabvnakryGTuohAlDSpk4tJyJQ8soK1DIkZ4p0Ijsp9j6DYTfmU3nvHl0vP8+8TVr9/i1DhDKz6etoID2okJihalboriYZHExTmkpTlERnkAA49n9H4eVe1O4tXiTEfyJEHmxFvLjreQnQgSSIYLJdoqcEGUmRIWnnUJPfG/ODMDmWAGro6WsjpayKlrGp9EyOh3/7l/Y1zqBhW4Xsb2EL0FHaQedJZ10FnfSUdJBPJjY6/N4414C0QDBeJCCZAFBG6TQFFJoCikyRRR7iyn2FhPwBfDs6dpM1TChGlLfuJ2zFmIOtMUsrVFLKAahOLQnPLQlvbQ5ebQToNMEd5qk60JR6kL1vLGsu6/OwVWFHDWsnGNHVHDyqCoGlQb38Lsh2U6BRmQvJdvaCL/zDuHZswm/884eBZi4x0NjYQEtpaW0V1QSqa4iWVUF1dV48nb+idOwfT+YXmUMSV+QpC9IJDBwl4fmOZ0EIpvJ79xCUWwLZYl6qmwDAzwtFHp67t8zMK+DgXkdHFe8CQDHwrpYCcs6K1geSd2aEvpjZLHEA3HCZeH0LVK88yaaz/LGvBRGCimOFVPqlFJuyqnwVlDpr6Q4rxj8pG59zBjI90J+0FAV/GxgSZIKRJ0kbTNNUcPmsMPmTqiP+Wl0grSZQhyz40//yoYwKxvCPD5/PZAKOCePquKkUdWcMLKSwnz9WctV+p8X2QPxLVtof30Gba++SvjddyG+8ysWCWPYUlREY1UlbYMGERsyBGpq8Pq3/6uSSeM/Yp4gsYLhUDCc+m2fsJZAso3CjnUUdW6gIr6BGmczg7xN+D7TNOUxMCw/xLD8EGezGoCGeJAlnZV82FnFRx3VtCRzo+tyLD9Ge2U7bRVthMvDxAO7vwJmHENBuICyaBmVTiXVppqavBrK88sx+Qby+6DwA8BroDpgqQ4YxgOQANpwbBsNUcOakMP6Th918SAtpniHVb63Bpz731lDntdw8qhqzj5sIGeOG0hlUYZ+U2SfGLuzYZnSZ4wx84866qij5s+f73Ypso1EYyOh554n9PzzdC5atNMhzHGPhw1lpdQPGkTH0KE4I0bgC+TGH+ad8dgExZ3rKQ2vpCK6nkHOBoZ4m/Dsps/IumgxH3ZWs7ijimWdlURtdnzmSnqThMvDtFW20VbRRrQouusXOFAYLub5obcAACAASURBVKQ8Uk61U81g32CGBIaQ78vtP9BxB9aFDStDsCYSpJ6SHq/iQCpATxpWzoVHDuGCCYPU96afmTRpEgsWLFhgrZ3UW+dUoOkHFGj6DycSoX3GDFqnP0X7W29BMtnjcXWFhdTV1NA6YgTO6FE5H2D2hN+JUBZeQWX7cgYl1jDUbCbf0/P3FyDuGD7qrGZBeCALwjUZd/UmFogRqgrROqCVcHkY69n5e60n4aGkvYTqWDUHmYMYnj+conytZr07cQdWt3tY1mpYEy2k1VPc43E+j+GMcQO4aOJBnDa2WsPE+wEFmiylQOO+2OrVNP/tEVr+8Q+cUGiH5x1gfWkpdcOG0nboofgHDUqNLpJ9ZmySss41VLd9RG1sBcM8dfiMs9PjP42UsiBcw4JwDetixbgyC94uWCydxZ2EqkOEqkN0luy806xJGkraSqiJ1jDCM4KhwaHk+3P76ktvaIoaFjd7WN4RpN6W9NjZuCzo40vHDuVrxw2jtqKgh7NIX1CgyVIKNO6wySTtM2fS/NeHCb/9do/HrC8uZt3IkYQnHE5+VVUfV5hbfE6MqvAyBrR9xLDkpwzytuz02I2xQua0D2FO22A2xnv+VN4XLJZIUYSWgS201LQQK9j5BIjB9iADOgYwjGGMCo6iIE9/TA+kcNLDwgbDh+0FNJmSHZ43wGljq/n65OFMGVWNZ3ftodKrFGiylAJN37KxGK1PP03jn+8mtmbNDs+35Ofz6dChtBwxAX9tra7EuKQw1kBNaCHDIh8xwmzEu5P5b9ZEi9Phpj5R2OMxvS1aEKVlYAvNNc077Q9jHENpaykHRQ9irH8sNYU1+llySUPUy7xGD0s6i1PDxD9j1IBCvnPqIVxwxGD83kzqrp+5FGiylAJN33A6Omh57DEa/3LvDjP0WmBVRQVrxx+GPeIIfP5+OF9KDstzOhjYtpiD2hYxilUEPD3PybKss5yZoaHMbR9MpJc7FCd9SVoGttA0pImO0o4ej/HEPVS2VjIiMYKxgbGUBkt7tQbZP46FZW0+5jTms8mW7fD8kNIA3z51JF88upaAX/1sDiQFmiylQHNg2ViM5kf/TsNdd5Fs2n4m0ojXy5LaWhqPnkT+0D2bzl3c5XViDGr/gGFt8xnFKvLMjh2LI0kv74YHMzNUy/JIBfva38ZiaS9vp2lIE60DWrHeHd8vTcJQ1VLFyMRIDi04lML8vrlKJPunMeZldr2PjyNlJM324be6KI8fnDWGy44+CJ+u2BwQCjRZSoHmwLDJJKHnnqP+9juIb9iw3XPtfj8fjxxJ6ITJ5Jft+ElNMoPfiTAo9D7D2+czyqzpsVlqU6yAN0LDmBkaSruzZ0N34/44TQc10TSkiVhwx34xJmkobynn4PjBjA+OpzjgXj8e2T+dScM7DXksaC8hZrb/+RheEeTH547jvMPVXNjbFGiylAJN7+uYN4+6X/430aVLt9sfysvjwzFj6Jx8PHlFGhabTQLJdmqbZzMuMo8aT/MOz0cdD++0D+HV1uGsju4YYi2WjpIOGmsbaalp6XGYdbAtyIj2ERyRfwRVheoknk1ijuG9Jj/vtpYQMduPOJswpIRffOFwjqzVh5/eokCTpRRoek98yxa2/O8thJ55Zrv9HT4fH4weRfikkxRksp21VMbWMrz5LQ5NfESwh3WolneW80rrcOa2DybugZaBLTQMbehxqLU35qWmpYbxjOeQ4kPw7MGaWpK54o5hdmMec0OlxE13XzoDXHb0Qfz7uWM1A3EvOBCBJjum4ZScZ5NJmh96iPo7/g8nHE7vj3s8LBo+jJYpp5BfUY7mCs0BxtCYP4zGmmG878SoDc3jsPa3GOLpXrRhdLCZgYUtJArX8HBpMR09rGBd2FrI6PBojiw8kqJSheBc4fdYTqmOcmxFPbPq81kYLsMxXizw6Lz1PL94E9d9bhxfPXaohnr3Mwo0kvGiK1ey6T9+klqeYBvLq6pYc9qpBGprM3WZG9lPSU8eq8tOYHXpZKqiqxnVPINys4KHywp5vLiITo+H1Bi3FJM0DGgawBHOEYwqGYUnoKsxuSrotZxTE+HYeD3PbypgTSI1l01bNMlPp3/IM+9v4JbLjtTkfP2IAo1kLJtM0nTf/dTffjs21t1xszEYYNGxx+KdOJGAmgcEwBiWB0v5W1Etyz0dOJ/pPDwwkeAroTYuDEVoCA5kUVElIf3sCFDuT/JPQ9tY3h7lxS3FtJNaguPd1c2c9ds3+MnUQ/naccN0taYfUKCRjBTfuJENP/oxnQsWpPcljWH+wSMInXkm+YUaOispzaaZud65LPcs32H09qBEgH9uDXFJqI6tvSWqO+YypuM9lgcnsbD4TNp8lX1es/Q/o4tiHFzQyIz6IO+1l4MxRBKWnz31ES8u3sRtX5nIgOLMWm8s2yjQSMZpe/VVNl7/U5zW1vS+usJCFp8yhcDYsWpeEgBaTEs6yNjPXJGppZYvHfwlvnLcV8jzeYl/9DTh139NYfPHAHiwjO2cx6jOBSwPHs3C4jNo91W48c+QfsTngbMGdnJYaYLpm4ppsalZh2evbOKc387ktq8cxSmjq12uMndplFM/oFFOe8aJxdhy869p/utfu/cZw3sHjyB89tn4gztOaS65J0SIub65LPUs3SHIjDQjuXLslZw/6Xy83s/MBGstiZWziLz4c4rqt/9dTOJhecExzC8+iw6vZv8VSFh4o76AuW1l2y2C+a0pI/jxOWO1hMJuaJST5KxEfT3rr/kene+/n97XmpfH3JNPInDEEWihAokQYb53Pou8i0h+ZvbgEWYEVx96NVOPmrrzYdfG4Bt5CkX/+jrJlbOIvPAzCusXAuDFYVzHuxzSMZ/FRaewqOhU4h41L+Qyn4EzB3QwsijB9LpSOrvGUP5p1ioWrW3mD5cfQ3mhxlX2JV2h6Qd0hWbXOhcvZv13r9lu/aVPKitZM/U8rYAtJEnygfcD5nnnETGR7Z4bboZz1biruGDSBfs0f0zy0zdSwaZh+xF0HaaABSXnsKTgOKzRmj+5Lpz08I+NxayNdw/vH1ySx1/++TjG1uy40rdoYr2spUCzc63PPMOm63+aHsXkAHPGjCF69llaQDLHWSwrPCuY7ZtNyIS2e66GGq4edTWXHHfJjk1Le/2FLMnlrxJ9fhoFrSu2e6rZU8nc0vNZEzhsu2YHyT3WwqzGAt4Olaf3BXyG2758FOeOr3Gxsv5JTU6SM6y1NP75bup/+9v0vojXy9uTJ+M/5mh8+uOR0xpNIzN9M9ng2X6NrhJbwlcP+ipXnXwV+fm91D3cGLxjzqJg1BnEFzyE8+ovyI+kJukrdxo5p/l+1uaNZnbZFwj51CE0VxkDp1R1UBNI8tSWMhL4iCQs33loPv91waFcceIIt0vMego00u9Yx2Hzr/6H5gcfTO9rCAZZcM7ZBA8+2MXKxG1Rosz1zmWRd9F2HX7zbT7nV5zPtadeS3lJ+S7OsB88HvxHfx2O+CLRWbfjnX07vmQHAENjyxm85TcsLjqFhUVnkPCo70SuGlMU5Yq8Rh7dUEabzccCNzzzMZtbO/n3z43TIpcHkAKN9CtOLMamadMIPf9Cet/akhKWXXwRwQoNm81VFstSz1Jm+2bTYTrS+401TA5M5j9O+Q+GDxreN8X4g+SfMQ2Ov5qO568n+NEjGCw+kkxsf51DwvOYU3YhqwIT1AyVowbkJfjm0Cb+tqGMzYnU6Mu7Zq1icyjCr794JD6NgDogFGik33BiMTZc8z3aZ85M71teVcXaSy4moInyclYrrbzuf531nvXb7a+llh9O/CFnHHGGO4UVVlLwxT9gT/wXOp+4hmDjYgCKbYizmh9idd4Y3i6/lLBXKzTnogKvw+UHNfPEJodV0dT715PvbyIcTfC7rx2tYd0HgL6j0i840Sjrr7lmuzCzaMgQ1n/pMs36m6McHBZ4F/Bw3sPbhZlCp5BvDf4W078y3b0wsw0zeCLBf51F4vw7iPu756gZHlvGpZv/l0PDb4N1XKxQ3JLnsVw2uIXDCtrS+15aUs//e/A94kn9TPQ2BRpx3dYwE545K71v3vBhNF9yMf7e6tgpGaXe1POY/zHe9r1NwiSAVPPSifkn8sT5T3DNWdeQl9eP+ql4PPiO/gb+f/uAzsO/lt6dT4yTWqdzQf2dlMU37+IEkq28Bi4cGOKoou6ReK8sbeA7D8xVqOllCjTiKhuPs+Ha7xOe9WZ633sjRtB+4YV4fWoRzTVJkszxzuFR/6Ns8WxJ76+yVfxq/K+460t3MaR6iIsV7kawjOAld2KvfJFo8bD07kGJtVxcfytHtL2O0dWanGMMnFPdxqTi7lDz6rJGrvnrPBxHU6f0FgUacY11HDb99D9pf+ON9L65I0YQvvAChZkc1GSaeNz/OO/53kuPYPJaL+cVn8dTlz7F1KOnZswIETNsMvnfm0vs+O/jdE285yPJcW0vMLX+9xQnGl2uUPqaMXB2VRtHbxNqXvy4np/+YxGaD653KNCIa7bc8htan3oqvT1/2DA6Lrxg/ydCk4xisSzyLOIR/yPbXZUZwhDuOPoObr74ZkqKMnC2VX+AvHN/jufbbxKpPDS9e3BiDRdv+Q1jwnNTs7FJzjAGzqpqY+I2zU8Pv7eBW19e6mJV2UOBRlzR+Jd7afrLX9LbH9bUEFKYyTnttPO0/2lm+Wel11/yWA8XlFzAE198ginjp7hcYS8YeBiB//cmsRN/jNP1lptPnFNaH+OsxnsJJNtdLlD6kjFwbnUbY4Ph9L47ZqzkoXdWuVhVdlCgkT7X9vrrbPnf/01vr6isYMvFF2kpgxyz2rOav+X9jbWetel9VbaK30z8DTdddBOFBVk0us3rI++sn+K5+tXt+taMiC3h4s23MCi6YhcvlmxjDHy+poVh+d1zKv3s6Y95e0W9i1VlPgUa6VORZcvZ+KMfpy+1ry8uZvXFF+MPaOXiXJEkydvet3nG/0z3YpIWpgSm8MRFT3DmEWe6W+CBNGQS+dfMIXbkFeldRYSZ2vAnJoZeVofhHOI18MVBLQzwpX4HHAvfuv89VjWEd/NK2RkFGukzicZG1n/nOzgdqU8lLfn5LLnwAvKLi12uTPpKG238w/8PFvgWpPcVOoX85JCf8LvLfkdFaQ7MBp1XQN4Xbsf56uPE81KT7nmM5Zj2Vzi34Y8Ek6HdnECyRZ7H8qXBzRSYOADhuOXyP79Na2fc5coykwKN9AmbSLDh+z8gvnEjADGvh/fOOpPAwIEuVyZ9ZbVnNY/kPcImz6b0vhFmBA+c+QBfOekrGTOCqbd4Rp+F/7tziA46Jr2vNr6Sizb/Vk1QOaTY53DZoGa8pK7OrW+N8/8eeFfDufeBAo30ifr/+x0d770HgAXePOZYAqNHu1uU9AmL5T3vezzj625iMtZwXvF5PHrZo4yuzeGfg5JB5F/1IokT/g1LKtAVEea8hj8xvn2WRkHliMGBOOcPaElvv72qld+9tszFijJTTgcaY8zJxpgnjDGbjDHRrvuXjTHn9XDsCcaY540xTcaYDmPMB8aY7xtjNCxnN9pnzaLxj39Mb88deTD+yce7WJH0lRgxXvC9wBzfHLr+XlPoFPKfo/+Tmy++mWAg6G6B/YHXh+/s/4LL/0E8L7VSuNdYTgg9w5Smv+G1an7IBYcVdXJsSXdz422vreDdlZqvaG/kbKAxxvwUmAVMAV4EfgM8A5QDp37m2M9vc+w/gDuBPOBW4JE+KzoDxTdtYuO/X5feXl1WRvjcc3OueSEXtdLK4/7H+dT7aXpfLbXcd8Z9fPGEL7pYWf9kRp6G/7vvEB1wRHrf2OhCpm75HYXJll28UrLFaZVtDM7r6iSM4TsPzKWhPepyVZkjJwONMeaLwI3Aq8DB1torrbU/sdZ+y1p7DHD9NseWAH8GksCp1tpvWmt/DBwJvANcaoz5ct//K/o/6zhsvG4ayZbUm3Gb388nU8/T+kw5YK1Zy6N5j9Lo6f6EeXze8TxyySOMHTrWxcr6uZJB5H/rFeLju99SapIb+cLmWxkY1Twl2c5r4OKaZgJd65c1RRyufWiuZhLeQzkXaIwxHuBmoAP4qrW27bPHWLvdNd5LgWrgEWvtvG2OiQA/7dr8zoGrOHM1P/ggHXPnAuAAc048QZ2Ac8BHno942v80UZP6ZOmxHr5W9TX+cNkfMnPG377my8d/yR9InntzetmEQjqY2vAHRna+73JxcqCV+Bw+P3Cb/jSrQzw8R2F2T+RcoAFOAEYAzwPNxpipxpjrjDHXGmMm93D86V33L/bw3CxSwegEY4wuO2wj+umnbPntrenthSOGkz9xonsFyQFnsbzjfYfX/a+n12IqcAr4+bifc93U6zQL9N4wBu/x38bzjWfSQ7t9xuGM5r8yIfSaOgtnuZEFUSYVd3/WvvHZJaxr6tjFKwRyM9BsHSO5GVgAPAv8D3AbMNsYM9MYU73N8WO67pd/9kTW2gSwCvABB+/uCxtj5vd0A7LqGryNx9l43TRsNPUJfXNBAS3nnKN+M1ksSZKXfS8zz5e+iEm1reZPU/7EF477gouVZbjhJ+L/zixipd1vL8e3v8iJzY9hbNLFwuRAO72yjXJvDIBIEr77oIZy704uBpoBXfffBoLAmUAxMB54iVTH38e2Ob606751J+fbur+sd8vMXI333kfkww8BSBjDB6edSl5BgctVyYESIcJ0/3SWe7sz/0gzkgenPsgRI4/YxStlj5QPI+/brxMbclx612GR9zi74W78TsTFwuRA8nssFw5swZAKMYs2dXDvW5qfaFdyMdBsve5tgEutta9Za9uttR8BFwHrgVN20vzUk62XHXYbna21k3q6AVmz1Gps/Xoafv/79Pa8UYcQGDNmF6+QTBYmzJP+J9no2Zjed4z/GB685EGGVA9xsbIsEywn78pniR96SXrXsPgKPrflLvKTmio/Ww0JxJlc1t30dMvLy9kSUojdmVwMNM1d9yuttYu2fcJa20nqKg3AsV33W6/AlNKzks8cl7OstdT94hfYSOoXbnNBAR1nZvG6PDmulVYez3t8u5FMU4um8scv/pHiQi1n0et8efi/eA/Jk36c3lXjbNSw7ix3UlkbZV1NT50JmPb3ebt5Re7KxUCzdfrFnb0DbA08W2f82nr8DtOZGmN8pDoYJ4CVvVVgpmp76SXCs94EUperFp90ohadzFKNppEn8p4gZFITgRlr+EbVN7jpopvwa9X0A8cYvGf+FGfqremZhatsA1M3/x8lCa3UnI18HjhvQPfn5ddXtPLax5t28YrclYuBZhapADLKGJPXw/Pju+5Xd92/3nV/bg/HTgEKgNnW2pye/cgJh9n83zeltxcPGULeYYe5WJEcKHWmjif8TxA2qaYOr/VyTe01/Gjqj/B4cvEtpe95jvlnuPQvOMYHQBkhzt/yOyriG3fzSslEw4MxDivsblr8yRPvE02oU/hn5dy7j7W2AXiUVBPSz7Z9zhhzFnAOqeajrcO0HwcagC8bY47e5tgA8MuuzbsOcNn9XuM995CoT31CbPf72XzWmRrVlIU2mo1M909PzzHjt36mjZrG1Wdc7XJluceMvxjPVx8l6UnNGFFEB1Prf09VbL3LlcmBcGZViHyTCjGbww5/fF1rPX1WzgWaLv8GrACuN8bMMsbcYox5DHiB1IzAV1trWwCstSHgalKdid8wxtxtjPk18D4wmVTgedSNf0R/Ed+0ica/3JveXnjYYQQqKlysSA6EjWYjT/ufJm5S804GnAA3jr+RL5+oibJdM+pMvFc8TdJfBECQKJ+r/4NCTRYq9DpMqejuIPz7mato1LII28nJQGOt3QIcR2otplrge6Qm0HsOONla+9hnjp8OnEKqueoS4BogTioYfdnm+LzUW269Nd0RuK6wkPhJJ7pckfS2z4aZoBPk5ok3M/XoqS5XJgw9Hu8/P08iLzU+IWgUarLVUSVhyn3dc9P891OaOXpbORloAKy1Tdbaf7PWjrDW5llrK621n7fWztnJ8W9ba8+z1pZba4PW2sOttbdam9uzW3UuXkzo6WfS2x8fewz+vJ66Jkmm6inM/ProX3P6kafv5pXSZwYdge/KZ0kq1GQ1r4EzK7uv0kxfXM/yutAuXpFbcjbQSO+ov/W29OMVlRV4j9BEatlkk9nUY5g59fBT3S1MdjToCLw9hJrK+AaXC5PedEhBhGGB7hW5b5y+0OWK+g8FGtlnHfPmEZ49G0gtPrnypJM0yiWLNJgGnvE/ozCTSXoINefW/5FSDenOGsbAGZXdV2XeXN3Oh+s1DxEo0Mh+qL/j/9KPl9YMJDhypIvVSG9qoYWn/E+lRzMFnAA3H3Wzwkwm2BpqujoKF9LJOVvu0uR7WaQmP86Ygu7FKn+pqzSAAo3so/Ccd+mYOxdIXZ3ZcKI6AmeLdtp5Ku8pOkzqDdNv/fxiwi847YjTXK5M9tigI/Be/gSONzWku4w2zt18F4Fku8uFSW85eZsRT3PWd7BwTZOL1fQPCjSyT+r/r/vqzJJBgwgMG+ZiNdJbOunkKf9T6RmAvdbLtNHT+Nykz7lcmey1ocfj+crD6cn3Kmni7C1/1IKWWWJAXoJxhd1XaW56WiOeFGhkr3UsWEDn/PkAJI1ho4ZpZ4UECZ71P0uTJ/VJz1jDNUOv4bITLnO5Mtlnh5yJ55I/p5dJqLF1nFH/Fzw24XJh0htOLm9j67rI723o5KMNud2sqEAje63xnr+kHy+tGUigttbFaqQ3WCyv+F6hzlO3dQdXDLyCb57+TXcLk/03/mI4v3s04tDkKk5o/Dvk9vRZWaEqL8HYgs709m+f/8DFatynQCN7JbpyFe2vv57e3nTMsbs4WjLFbO9sVnhXpLc/X/p5vn/O912sSHqTOfoKnFN/kt4+NLaQI1pfdrEi6S3Hl3X3i5rxaYgNzR27ODq7KdDIXmm69970J7uVFRXkjTzY5Ypkfy32LGaBb0F6e3LeZG644AYNwc8ynlP+neSE7mUqjut4lZHheS5WJL1hcCBObX73vDR3vJi7V2n0jiV7LNHQQOv06entNUdN1AKUGW6VZxUzfTPT26M9o7n187fi8/lcrEoOCGPwfv53JIdNSe86peUxBkU/dbEo6Q2Ty7uv0kxf3EBrZ9zFatyjQCN7rOWxx7Dx1C/KxqIizKGHulyR7I8m08RLvpewJnXFbaAdyJ3n3UlhQaHLlckB4/Xj/cpDJCpGA+AzDqc33EdxQkN+M9nIYJRKf2qNp6hjeGBWbq7ErUAje8QmEjQ/+vf09qfjxuLVp/iMFSXKc77n0rMAFzvF3H7K7dRU1rhcmRxwgVJ8X3+SZLAKgEIT4fQtd+NzYi4XJvvKGDimNJzefnjuWnJxzWQFGtkj7TNnkqhLjYAJ+3zEjz7a5YpkXzk4vOR7iRZPaoinz/r42YSfcdiIw1yuTPpMWS3er/4Nx+MHYCD1nNjwV418ymDjizrJMw4Am8KWmUs3uVxR31OgkT3S/PDf0o+XDx2KPxh0sRrZH3O8c1jjXZPevnLQlZw76VwXKxJX1B6L5/zfpjfHJD7m8NCrLhYk+yPPYzm8uHuE059eX+piNe5QoJHdiq1ZQ/jtt4HUFE6Nk45ytyDZZ594PmG+b356+5TAKXz3rO+6WJG46qiv4xx9VXrzuPaXOajzYxcLkv1xVEl3s9OcdR1sDuXWrNAKNLJbLU88mX68qqKcfE2kl5GaTTOv+V5Lbx9sDubmC27W8Owc5/nc/5CsnZx6bOCUpocpTDS7XJXsi+q8BAdtM4T73hm5FU71Tia7ZB2H1qefTm+vGzvOxWpkXyVI8ILvhXQn4FKnlNvPul0jmiQ18unLD5EsTHUILzRRTqm/D2OTLhcm+2JiSXez09Mf1OVU52AFGtmljnffTXcG7vD5SB4xweWKZF/M8s2i0dMIpBacvH7C9QwfNNzdoqT/KKzC+6UHsMYLwEF2I0c1Pb2bF0l/NKYwgr+rc/DGsGX+6gaXK+o7CjSyS63Tn0o/XjF4kDoDZ6BlnmV85P0ovX1p5aVaPVt2NPQ4zJn/ld6cFJ1NbceHLhYk+yLPYxlb2L2+0wMzc6dzsAKN7JQTDhN65ZX0dsP48S5WI/ui2TQzwzcjvX2Y9zCuO/c6FyuSfm3yNTiHnJXePKX5EYrUnybjbDva6bUVrcQSjovV9B0FGtmpttdew3akfjEaggG8o0a5XJHsjSRJXvK9lO43U2bL+M05v8Hv97tcmfRbHg+ei/9EsmgQAAUmysn1D2BsbvxBzBbDAjGKvQkAwgnDi4vWulxR31CgkZ0KvfBi+vGqYcPweL0uViN7a653LvWeegA81sP1h1/PkOohLlcl/V5BxXb9aWrteg5r1fw0mcQYOLy4u9npibmrXKym7yjQSI+S7e2E33orvR06TLPIZpKNZiPzvd3zzVxQeoEmz5M9V3ssTPlRevPY8GtUxNa7WJDsrXHb9KOZsy5MNJH9o9YUaKRH7TPeSC9EubmgAJ/mnskYMWK84n8lvejkMIZx/eeud7kqyTRmyo9JDpoIpBaxnFL/IF6bm6s4Z6IBeXHKfKn/r6hjeDkHmp0UaKRHbS+/lH68vrZWk69lkFm+WYRMCIA8m8cvT/olwYBGp8le8vrxXnoPji8AwADTxMTGp3bzIukvjIFxhd0zBT/53mr3iukj+islO3DCYdpnvZnebjnsUBerkb2xyrOKJd4l6e3LB13OkSOPdLEiyWiVI/Gc+6v05lGxd6np/MTFgmRvjC3avtkp20c7KdDIDtrffBMbjQJQHwziGzrU5YpkT0SJ7jBE+7tnaJ0m2U+TrsQ55Oz05glNj+J1Yi4WJHuqJi9OSddop86kYcbHG1yu6MBSoJEdtL8xM/143ZAham7KELN9swmb1OJ0QSfIjafeiM/nc7kqyXjG4Lnw35a/kwAAIABJREFUDpy8YgCqTCtHND3nclGyJ4xJzRy81XMLVrtXTB/QXyrZjnUc2t/sbm76/+zdeXxd13XY+986d8AMEABBgDMpkiIlStRozZIleYjtOnHs2Kljx7OfkzR2EifxS5rBcZo282ubJk76mrSW0zZz4zjzKFu2lciyZE3WYIkSKc4EiXm+0+of5+KeDQjEeIB97z3r+/nww3OBA5wligQW1l577ZED+z1GY5brlJziG6loqut7d7yXAztsbpCJSftWgjf8fOXl9TP/QvdM/TeZ1oP9zVFC88/HR+v6bCdLaMwc008/Q3EgPPNnIp2G/ZbQVLs8ee5P3195fTA4yPfc/T0eIzJ16br3UNp9JwCBKLdf/D0CLXgOyixlZ9NM5Wyni9Nw9Pyo54jWjyU0Zo7xLznLTT09pG2qbNV7OPUwI8EIEO5q+tQdn7JpwCZ+IgRv+XVKqXDXU58McHjYBu5Vu7TA3qaZyuvPP3zUYzTryxIaM8f4A1+qXA/s2e0xErMcAzLAY6nHKq/f0fMOrtprZ26ZddK1l+C1n6y8vGHyi7QVBjwGZJZjn7Ps9MXn6/f0bUtoTEVhcJDpp54CoARMHzrkNyCzKEV5IP1AZYDeTnbyQ6/5Ic9Rmbp38/dS6jsCQFaK3HDhjz0HZJbiJjTPDuSZmKnPpUJLaEzF5MMPQ7lh7GxbG9nOTs8RmcU8HzzP6SDchikq/Oh1P0pjY6PnqEzdC1IEb/7PKALA5foi2yee8hyUWUx7ukRPJtxqX1ThgWfq8xgLS2hMxcRXv1q57u/r9RiJWUqOHF9JR2dt3dF0B/ceuddjRCZRdtwA17+38vLWoc/ZsQhVbndTNDvo/m9YQmPq3ORDUUIzttv6Z6rZV1NfZVImAWjRFn7q3p/yHJFJGnnNz1Bq2ARAVzDG4cG/W+IjjE97nMbgR07W504nS2gMAPnz/eSOhUfMF0Qo2nbtqjUogzyReqLy+t3b3822nm0eIzKJ1NJN8LpPVV7eMP1l2gqD/uIxi9rZOAOELQUvj5YYmaq/ac+W0Big3D9Tdra9nXRzs8dozGK+kvpKpRF4F7v4nlfbzBnjyfXvo7Q1PCssIyWuufg5zwGZS2lKKX3ZcFlQEe5/qv4GI1pCYwCYfDhabrrQ1+cxErOYE3KCl1Mvhy8UfvDID5LNZv0GZZIrCAje+MuVl1eWnmPz9DGPAZnF7HaWnb74zBmPkawPS2gMAJMPf61ybf0z1alEaU4j8PXZ63ndta/zGJExwK6b0SveUnl548DnKrslTXVxE5rHTo97jGR9WEJjKAwNkXs5/Km/KELpsr2eIzILeS54joEgHGKW1jSfuO0TiIjnqIwBed2n0CA8CHWXnGXXxGNLfITxYUdD1DdzaqzEZK6+5tFYQmOYeiJqMD3f2mL9M1UoT56H0g9VXt/bdi9X7bGJwKZKdF2G3BT1cr1q+K/snKcq1JhSujNhH00J4aHnz3qOKF6W0BimHn+8cj2webPHSMylPJ56nAmZAKBZm/nE3Z/wHJEx89z1o5QaOgDoDkY5MPJlzwGZhexojKo0//zcaY+RxM8SGjOnQjO2davHSMxCppnm66mvV16/bcvb6Ou2xm1TZZq7CO7+scrL68a/QKpUf1uDa902Z9npsZMjHiOJnyU0CafFItNPPFl5PbNnj79gzIIeTz1OTsIvQpt0E9931/d5jsiYS7jxQ5Raw2S7PZjiwPAX/cZjXmG7U6F5fjCP1lEDtyU0CTdz9CilyXDi7FgmQ9DT4zki45piisdT0ZLgd27/Ttpb2z1GZMwiMo24VZrrJ79EpjR96fvNhtucKZCVEgBjeeHli/Wz28kSmoSbejKqzvRv2kSQSnmMxsz3aOpR8hI28XVrNx++88OeIzJmCdd+N6WOXQC0BjNcPvhPngMyrkBgm1Ol+fIzJz1GEy9LaBJu5tlnK9fDm7s9RmLmm2CCJ1NRwvmu3e+iqbHJY0TGLEM6S3DPv628vH76QRpKkx4DMvNtzUYHiT5xYsBjJPGyhCbhpp99rnI91WuNptXk0dSjFKUIwBbdwvtue5/niIxZpqu/k1JXeB5cU5Dn8oF/9ByQcfU2RAnNN8/bkpOpA1osMv3Nb1Ze53fu8BiNcU0xxdOppyuvv3vvd9PQ0OAxImNWIJWeU6W5Zuar1ktTRXqdCs2x4aLHSOJlCU2C5U6cQMsNweOZDCmbQVM1nkg9QUHCwWQ92sO7bnmX54iMWaHDb6XUeRkAzUGOfUMPeA7IzOrMFMiUG4PHC8LZoQnPEcXDEpoEm3kuWm4aaGuzMfpVIkeOJ1LRbKB37HqHVWdM7QlSBHd+vPLy2qkHSWl+kQ8wGyUQ2OJUaR5+oT4OqrSEJsGmn3Eagrs6PUZiXE+lnpozd+Z9t1rvjKlRR95JqW0bEM6l2Tv8oOeAzCy3j+ax4xc9RhIfS2gSbNqp0Exs2eIxEjOrQGHO3Jlv6/s2mpvsbC1To9JZgts+Vnl5zcQDiNZPz0Ytc/tonjs35jGS+FhCk2AzLx6tXOf6bIdTNXg2eJZJCfuaWrWVj9zxEc8RGbNGN7yPUmNYAe4Oxtk19ojngAzMXXJ6ebg+jqiwhCahShMTFM6EJ62WALWExjtF51RnvqX7W+ho7fAYkTExyLYQ3PpvKi8Pj34R6mjcfq3qzkanofdPQaFY8hhNPCyhSaiZY8cr10NNjaQbG/0FYwB4OXiZ4WAYgKxm+cgtVp0xdeLGD6GpsLF9R3CRzVMveg7INAZKaypc/iuqcPTcsOeI1s4SmoTKvRR9QRlpbfMYiZnlVmduabmFbT3bPEZjTIxaupFr3ll5eXDIjkOoBt2ZaNnpyePnPUYSD0toEmrmxZcq1+ObbFnDtwEZ4GQQnqkiKnzo+g95jsiYmN0SnRJ/BUdpydfPyP1atdlZdnr29JDHSOJhCU1C5V6KEpqpri6PkRhgztyZQ+lDXL/veo/RGLMOtlyBXnYPEM5B2Tdwv+eATHcmSmhevFD7w/UsoUmoGSehmemxLds+TTHFc0G0hf67Lv8uj9EYs37klqg5+EjhMdKlGY/RmM3OTqcTdbDTyRKaBNJCgdyJE5XXhb5ej9GYZ1LPzDmE8s3XvdlzRMask/2vRbv2AdAc5Nk9/C+eA0o2t0JzbkLRGt99ZglNAuXPnYd8mJmPZzKk26wp2BdFeTqIDqF809Y3kclkPEZkzDoKAuSmaPfeocmHbAu3R62pUuVMp+mSMDRR2xUzS2gSKH/qZOV6tKnJznDy6JScYiQYAcKt2u951Xs8R2TMOrvmX1e2cG8PBuiaedlzQMklApvS0eTm507V9hEIltAkUP7Uqcr1REuLx0jMN1LfqFzf2HwjW7qsn8nUuaZO5KrvqLy8bNBO4fZpk7Ps9MKZ2t7pZAlNAuVORgnNpC03eTPJJC8FUXP2d11pzcAmIW54f+XycOlZMqVpf7EknFuhOXahts90soQmgdwKzYzNoPHm2dSzlMrr19vYxl1X3uU5ImM2yM6b0J4rAGgIiuy05mBvOpwKzcnBSY+RrJ0lNAmUc3pocjaDxov5zcBv3PZGgsD+OZqEEEFu/EDl5ZWTX/UYTLJ1OhWaM6O1vXXbvoImUP7U6cp1sbvbYyTJdVbOzmkGfveN7/YckTEb7Mh3VpqDtwUDbJo+ucQHmPXg9tD0TxYXubP6WUKTMKXJSYoD4cjxoghqFRovnktFg/SubbyWns4ej9EY40FTJ3LFt1Ze7hr6Z4/BJFeHU6EZmhGKpdrdRm8JTcLkz0cHkI1ls6Rs5smGK1DgheCFyutvP/DtHqMxxqNrokb4K4vfQLS2KwS1KBsoTUH4515CODdcu0cgWEKTMIXz/ZXricYGj5Ek17HgGDkJ16o7tIM3HHmD54iM8eSyu9GWcFRBezBN7/gzfuNJqLZ0qXJ97Fztbt22hCZhCv1RhWaqqcljJMnlntt0R+cdNhnYJFcqjRz5zsrLPSMPeQwmudpSUWXs5MVRj5GsjSU0CeMuOU0321C9jTbJJC8H0WTUdxx+h8dojKkCzrLTIXnRZtJ40Ob00ZwesiUnUyPcJadca6vHSJLp+dTzqIRNdzvYwfX7rvcckTGe9V2F9l4FQFaKbB/5mueAkqfVqdCcG57yGMnaWEKTMIV+J6Fps4Rmo7nNwPf03mPnaBkDyDXvrFzvmXjMYyTJ5FZozo/V7gGVltAkTMFZciq0t3uMJHnGGONccA4AUeE7jnzHEh9hTEIcfmvlcp+coqFUu8setchNaAYmCovcWd0soUmYvFOhKXZs8hhJ8hxNHa1c703tZd+2fR6jMaaKdOxAd7wKgJQovUOPeA4oWdpS0S6nwena3TpvCU2CqCqFCxei152W0Gyko0GU0Ly679UeIzGm+ohTpbls8nGPkSRPq1OhGanh0w8soUmQ0tgYFMJy4kwQEDQ2eo4oOeYvN7316rcu8RHGJMyVb6lc7gtOky2OewwmWZqCEhBuVpgqBhSKpcU/oEpZQpMgxaFoYNJUJmMNqRto/nLT3r69HqMxpgrNW3bqG37Uc0DJEchsUhPqr9FpwZbQJEhhcLByPZ3Neowkedzlprv67vIYiTHVS66MjgG5bOoJj5EkT5PTR3NmcMxjJKtnCU2CFIeGK9czltBsmAkm5iw3ffthO7vJmAU5y06XySkypdqdiVJrmp2Epn/EKjSmyhWHogrNjPXPbJjjwfHK9c5gp+1uMuZSNu1Et14DQFqULSNPeg4oOZrdJaeRSY+RrF46jk8iIpcDrwXuAnYBm4EpoB94HPgCcL+q2kxrj9wempwdTLlhjgXHKtc3b77ZYyTGVD+5/I1wNlxu2j7xFKc77d/MRnArNANjtfmtek0JjYi8E/g3wO2zb1rgttcAPwwMi8h9wK+r6vG1PNesTmEwSmgKdjDlhihQ4GRwsvL6jQfe6DEaY2rAwTfAA78IwH6O8TUtopLyHFT9cxOai+O1OS14VUtOInKPiDwG/B5wFfBZ4CPAtUAfkAU6gMuANwE/B3wT+DjwrIj8kojYmNoN5lZo8pbQbIiTwUkKEm6V76KLG/bd4DkiY6rc1mvRtj4AWoMcXZMveg4oGdxdTkOTeY+RrN5qe2j+CSgC/xroU9UPqup/V9UnVbVfVQuqOqaqx1X1b1X1U6p6G3AQ+E3go8APxvOfYJarOBw1BReamj1Gkhxu/8y1bdcSBNa2ZsyiRJDL31B5uXXEznbaCO4up5Hp2jz+YLVfXd+uqjeq6h+r6rLnCqrqC6r6I8A+4B9W+WyzSqWxaCteqdkqNOtN0Tn9M/fuvtdjNMbUkMujpdl9xRcWudHEpdGp0EzM1ObxB6tKaFT1T9fyUFU9p6oPreVzmJUrTkRb8Uq2y2ndXZSLTEj4Z96gDbz2ytd6jsiYGnHZq9F0+DWqNzVCa65/iQ8wa5V1EprJvE0KNlWuNO6MEm+0Cs16OxGcqFwfzB6kpanFYzTG1JBME7I3Ou+s27Zvr7uGQCvXUwVd5M7qFUtCIyJ7RORNItLivC0tIj8rIk+IyD+LiB1e45m75KS25LTu3N1Nr9ryKo+RGFOD9kVLtNunn/cYSDI0uBWa2myhia1C8zPA/wTcvV4/Bfw0cDVwC/BHInJLTM8zK6Sqc5acsF1O66pAgTNypvL69Ze/3mM0xtSgffdEl3IK0drs66gVboWmRltoYktobgX+SVULACISEM6neY5w0N5NwAThtm3jgeZykA+34hVEkAYbrLeezsgZihJ+Veimmyt2XuE5ImNqzObL0batADQFeTonjy3xAWYt3ArNdFFQrb1lp7gSml7gZef1tYTTgj+tqqdU9RHg84DV3T1x+2dyKRtStd7c/pnDrYftZHNjVkoE2feaysvNo095DKb+pQVShElMCWFqpvZm0cSV0GQAN527vfz6fudtp4CtMT3PrJDbP5NLx3LihVmE2z9z27bbPEZiTA1zlp125W3A3npzdzoNjtfewaBxJTSngCPO6zcBF1X1WedtW4DRmJ5nVqg4HvXP5NJWoVlPk0xyMbgIQKABrzn4miU+whizIGen0+5UP5lSbZ4xVCsanT6aofHa+7OOK6H5S+B1IvKrIvLvgdcBfz7vnkPMXZYyG0inotNTCymr0KynU8GpyvX2YDt9XX0eozGmhrX2QF/4s3JKlK6xZ5f4ALMWGSehGZ9a9szcqhFXQvPLwDHCQyh/AjhLuPMJABHZDdwGfCmm55kVKs1EfzmL1kOzrs4E0e6mqzuu9hiJMXVg712Vy+4J2769ntISJTSTSe2hUdV+wu3Z31b+daWqnnFuaSVMdn4njueZldOZqHxoCc36Oi2nK9c3b7/ZYyTG1IFdt1YudxSsyL+eaj2hiW3tQVWnCJeeFnrf08DTcT3LrJzORCOCLKFZP1NMMRgMAmH/zN2X3+03IGNqnZvQpC6SKuUoBlmPAdUvN6GZytXedL3Yjz4QkUMi8lYReU/cn9usXmnaEpqN4C43bQ220tXe5TEaY+pASzf0hHOc0qJ0jNmy03qZU6HJ1V6FJraERkSuFZFHCCsxfwLc57zv1SIyKSLfGtfzzMpoLkpo1HY5rRt3OvAVbTZMz5hY7I6qND3WR7Nu3IRmOqkVGhG5HPgicBD4NeBv5t3yJWAQeHsczzMrV5p2e2hsl9N6cSs0N227yWMkxtSR3bdXLrdZH826mZPQ5Gvv/IM4z3LKAjep6g8DX3PfqeEM5X/BJgV7o+6Sk1Vo1kWOHBfkQvhC4c7L7vQbkDH1wumj2RWcJ9Daqx7UgrR74naCE5rXAH86b5DefCeAbTE9z6yQu+RUsgrNujgn59DyTzhbZAs7enZ4jsiYOtGxHd20G4CGoEjHpFVp1oNboZnJlxa5szrFldBsIpwWvNSzrDXdE7cpuGQVmnVxPjhfud7fvN9jJMbUH9kZjUDoGD/qMZL6NSehKSQ3oekHlvoKfhg4ucQ9Zp1oIepY18ASmvVwXqKE5qruqzxGYkwd2n5D5bInZxWa9ZByztDNF5Ob0NwPfKuIHFzonSLyKsJlqb+L6XlmpZy/nBrYyc9xU3ROheamXdYQbEysdtxYudym5zwGUr/c7wzFkl7yvmoVV0LzC0AB+JKIfB/lXhkROVx+/RfAGPCrMT3PrJCWnAavIPbxQ4k3xhiTEp6XldEM1+2+znNExtSZ3qvQIBNepsfIFMY9B1R/AqIkplhKaIVGVb8JfAdhj8xvAB8mTPaeBD5dfvvbVPVEHM8zq+CWDy2hiZ1bndmR3kE2Y+1ixsQq04j0RWejtVsfTezEKdHUYoUmzqMP/lZE9gLvA24BuoER4CHgM6o6GNezzMpZhWZ9uf0zl7dd7jESY+rY9hvgzNcB6Jo8xsCmaz0HVF/c7ww1mM/El9AAqOow4WC9X4vz85oYuD00Yj00cXMrNEd6jniMxJg6tv0G+NpvA9BbOMkLnsOpNyLuklPtZTT2o3pSOBUaFfvfHqcSJfqlv/L6lt23eIzGmDrmNAbvkH7Q2vumW83cH3VLNfhnG+dZToGIfExEHhKREREpOO+7TkR+s3xEgvFA5/TQWIUmTsMyTKH8171FW9i/1WbQGLMuuvah2VYA2lMzNBZGPAdUX2p9ySmus5yywD8A/xnYR7ijyf2ueQz4IPDuOJ5nVmFOhcYSmjhdlIuV622ZbQTWo2TM+ggCpDea8dQy/pLHYOrPnCWnBFdoPgHcA/ws0Av8jvvOcm/Nl4Bviel5ZoV0Tg+NfcONk5vQ7G3d6zESYxKgL0poNk3ZrNY4zanQ1N6u7dgSmncDD6rqv1PVErBQancM2BXT88xKldyExmMcdchNaK7svtJjJMYkgLN1u7tw1mMg9cct3tdefSa+hGYv4fbsxQwCXTE9z6yUswwiWEYTp4tBlNBcs+0aj5EYkwC9UULTxwWPgdQfd5WpFr9LxJXQTBEeULmYXcBwTM8zK+U0AksNro1Wq0kmmZAJANKa5uodVy/xEcaYNdlyRWXZfEtqlFRxZokPMMvlfmeoxVbLuBKax4HXl5uDX0FEOgj7Zx6O6XlmhcTtm9EaXBytUu5y05ZgCw3ZBo/RGJMA2WakO9xJGAi0TNpBlXFxE5pa7LSMK+bfBnYC/1tE2t13iMgm4D6gE/ivMT3PrJS75GQVmti4y027m3Z7jMSYBHGPQJi0E3Xiok6DZWIrNKr6+8BnCM9zugB8H4CIPAKcBd4C/Kaq/nUczzMrJyk3ofEYSJ0ZkIHK9b6OfR4jMSZBnK3bnXlrDI7LnApNDWY0sVWVVPVDhLNmngF6CHuKrgeOAh9S1Y/F9SyzCrbktC4GJTqi7IqeKzxGYkyC9ByqXHaXrDE4LnMTGm9hrFrcZzndB9wnIk2ES0wjqjoR5zPMKrnD3mzJKRaKMiRDldeHtx72GI0xCbI5GjrfI7bXJC5WoQFE5H+IyMdnX6vqlKqesWSmitgup9hNMEFe8gA0aAN7evb4DciYpOjcg6bCPSidqSnSBftWEwfroQm9C9gS0+cy60CCVPSiFg/pqELuclNPqodUKrXI3caY2KTSSFfUs9Y8edpjMPXD/c6QqsE1p7gSmuNYQlPd3L+c1kMTC3e5aXvjdo+RGJNAPdGyU8uUJTRxsCWn0O8BbxSRzpg+n4mZW6GRWjykowoNBVFCs7vNtmwbs6GcPpqO/HmPgdQPt3if5ArNLwCPAF8QkTeLSG9Mn9fERLLRzEMpFhe50yyXu+S0v2u/x0iMSaDNByuXXUXb6RSHgtNDk03V3mi9uHY5TZd/F+DzALJwuUpVNdadVWZ5pCGaYBsULKGJg7vkdGWvHUppzIbqcXc6DS1yo1muopvQpGuvQhNXcvFlavNwzsSQbKZyHViFZs1y5JiUSQACDTjYd3CJjzDGxKr7QHSZGke0iIo15q+FVWgAVb07js9j1o+75GQJzdqNyEjlepNsorGh0WM0xiRQthlae2H8PGlRGmYuMt1o3Q5rMadCk6m95LD2UjCzKoGb0JQsoVmrURmtXG9Ob/YYiTEJ1rm3ctk4ec5jIPWh6Kyz1GKFpvYiNqtiFZp4uRWavqY+j5EYk2CdeyqXLbl+f3HUCXfJqSFTe+lBLEtOIvLJZdxWAkaBZ4EHVDUXx7PN8kjWaQq2hGbN3ArN9labQWOMF05C01a46C+OOuEmNI01uOQUV1Pwp5jbFOy2R89/uwIDIvIDqvoHMT3fLGFuhcbm0KyVW6HZ3WEzaIzxoitacmov2k6ntSrOSWhqb0NyXDWlewi3a+eB/w68H3hj+ff/UX77nwHvAH4RaAT+p4jcGdPzzRJsySleI0QJzb7N+xa50xizbpwKTZfzb9KsjvudoaEGE5q4It4NvA54lao+Ne99vysivwE8CHxOVX9SRP4AeBT4UcIt32adzdm2bU3Ba1KixJiMVV4f6DmwyN3GmHXjJDTdqbFL32eWpdaXnOKq0Hwc+KMFkhkAVPUJ4I+BHy6/fgr4K+DWmJ5vlhA4g/VSVqFZk3HGKUm4bNeszXS3d3uOyJiEau1F000AtAR5MoVxzwHVNnfJqakhs8id1SmuhOYgsNSeuTPl+2a9AGyK6flmCUFzc+U6bZOC18StznQGdnyZMd6IIJ1RD1vDlO10WotcKUpo2hqTm9CMsXS15TbATZ9byh9nNoDMSWgKHiOpfeMS/TXuynZ5jMQYQ/u2ymXDjO10Wou8m9A0NSxyZ3WKK6H5a+DVIvLzItLivkNEWkTkF4C7yvfNugo4HtPzzRKC5uh/S8aWnNbETWh6Gns8RmKMoT0am9CUt51Oa5HTKCVob84ucmd1iiuh+bfACeDHgJMi8kUR+UMR+SJwcvbtwE8AiMhWYD/hzifvROQ9IqLlXx++xD1vLv93jYjIuIh8VUTet9GxrlbQElVospbQrImb0PQ226h1Y7xyEprm4rDHQGqb6rwlpxqs0MR1ltM5EbmJcEv2OwmrMbOmgPuAH1fV/vL9Z4GqmEYmIjuBXydcDmu9xD0fLd8zAPwvIAe8HbhPRK5W1R/doHBXze2hsQrN2ow7K6dbW7d6jMQY4y45tRZt6/ZqFYFSeYRcgNJSgwlNbLONVfWCqn6IsNH3CHAncA2wSVU/OJvMVBMREeAzhInKf73EPXuAXwUGgRtV9ftV9eOE/40vAj8iIlW/W0uyWUiF2/DSqoglNavmVmh2bNrhMRJjjFuhabO2zFXLlaJ0IBsoqVRyt21XqGpeVb+hqg+q6lOqmo/7GTH6AeBe4APAxCXu+SDQAPyGqh6ffaOqDgE/X375vesYYyxEZE6VRmZmPEZT29yEZlfnLo+RGGPcCk2HXOrLuFmK2xCcDXSRO6tXrAmNiGRE5A0i8nER+Wnn7Y0iskVEqua0KxG5gnCJ7NdU9UuL3Hpv+fe/XeB9fzPvnqrmJjRMT/sLpIYVKTLJZPhCYVe3JTTGeOUkNJ3BZNgMYlYs5x5MWXvFGSC+ScGIyBsIjz3oIzqz6efK776WcFLwdwO/H9czV0tE0sD/JGxk/oklbp+dnfP8/Heo6lkRmQB2iEizqk4u8dxHL/GuQ0vEEIs5FZppq9CsxgQTlZPKWmihKdvkNyBjkq6xA820IPkJGoIi6eIEhfSC7ZBmEW5DcGONJjSxVExE5EbCHUtKODX499z3q+pDwDHgrXE8LwafBK4D3q+qU0vc21H+/VLdZiPz7qtacyo0M1ahWY0Jp6TdHrR7jMQYA4TD9dxZNNM2i2Y13C3bjWlZ5M7qFVeF5qeBScKm2XMi8jML3PM14PqYnrdq5d1YPwH8f6r6L3F8yvLvS9Y5VfWGS8T0KBvwZ+MmNMHMDNYWvHKTEhXhOtJVn8MakwytW2DgBQAyOdvptBpuD01jumq6Q1YkrqhvB/5MVRc7/uAk4HWPq7PU9DxhErYcS1VgZn9MH11DaBsiaImG64n10KzKFFGMgWpHAAAgAElEQVRBryNrCY0xVaFlc+Uym7eEZjVmnISmKZPshKYVWKrO1xzj81arFbgcuAKYdobpKTBbVfrt8tv+c/n1N8u/Xz7/k5UHBLYAp5bqn6kGQXtb5TplCc2qTEmU0HQ12LEHxlSFlmhid0Ox6n+2rErTzrbt1gbf36pXJ64lp9PA4SXuuRZ4KabnrdYMYePyQq4n7Kv5CmESM7scdT9hBeoNzttmvdG5p+ql2qOKQtoSmlWp7HACuhotoTGmKjgJTVPRTtxeDTehaW+Ibb/Qhoor6r8BvldE7lDVr8x/p4i8kfBwyl+M6XmrUm4AvtTRBp8iTGg+q6q/47zrM8D/C3xURD4zO4tGRDqJdkgtOJSv2qTaoybWlO1yWhW3QrO5efMidxpjNoyb0KjNolmN6aKT0DTVZkITV13pF4Bh4O9F5JeAKwFE5F+VX/8xcBb4jzE9b8Oo6jHgE0AX8IiIfFpE/hPwJLCP+JqL112qI0poMrbLaVXchKan1Q6mNKYqOAlNsyU0qzLt9NBsqsGDKSG+s5xOi8jrgT8i/OY/688JdwG9CLxNVWtyP52q/rqIHAd+FHgvYSL4DPBTqvpZn7GtRNAWJTRpmxS8Ku6SU2+rHUxpTFVwEpoWlprEYRYy4yw5dTQlOKEBUNWvi8hB4F8BtwLdhDuEHgI+r6qFuJ61HlT1U8CnFnn/XwB/sVHxrAe3QpOdyXmMpHa5FZq+9j6PkRhjKpyEpk0soVmNKSeh6Wpt9BjJ6sW6UKaqRcKqzJ/H+XlNPNwemky+mo/Yqk4lSnO2bfd2WIXGmKrgbNtuC2w5fTXcpuDO1to7aRv8b6M2Gyhwdjll81ahWakZZipjFLOatWMPjKkWjR2ohPP6G4MiUrIf2FZquhj10Gxub1nkzuq1qgqNiLx3tQ9U1d9d7ceatXGXnBryVb0CWJVyRElgk1gyY0zVEEEaO2BqEIBUfpxCQ6fnoGqL20Ozub02v76tdsnpPuaO+heWHv0/e48lNJ6k2qLBeg225LRiMxI1UjcFtfkP3pi6ZQnNqhU1OstJULraElShAT6wwNveBnwr8ADwReAc4cnb9wB3EfbVfG6VzzMxkOZmSKehUCCjihQKaLo25w34ME20Nt8cNC9ypzFmwzU6g0MLE9g+zuVz+2caAyWbzXiMZvVW9d1s/lZlEXkT4STdt5R3A7l+VkTeQriluyYG0NUrESHV3k5xMPwpRsbH0U2bPEdVO3ISLTm1pGrzJxhj6lZT9LUsXbBZNCvhDtVrSi95znLViqsp+CeBzy2QzACgqp8H/ozlHwhp1kmqKyrDyriNCF+JGednvpa0JTTGVBWnQpMpVv3RelVl0qnQtGVkkTurW1wJzTXA0SXuOQociel5ZpXSndH5Q8GYJTQr4fbQtGZaPUZijHkFJ6HJWkKzIpNOhaYtawlNjjCpWcw1gHWiepbqihKa9IQlNCvhVmjasm2L3GmM2XBuQlOyhGYl3ISmozHlMZK1iSuh+SfgTSLyURGZk95J6GOEJ1P/Y0zPM6uU7nYTGvtHvxJuhaY9277IncaYDecmNGrD9VbCTWg6m2t3o0hckf844W6mXwN+SES+ApwHeoE7gL3AYPk+41HKWXJKT1pCsxJWoTGmijVGTcENltCsyEQxqsp01ejBlBDf4ZQvisgtwG8CrwUum3fLPwDfr6ovxfE8s3puU3B2ys48WYm8s2La2mA9NMZUlWzUqJ9Rm4S+Em6FZnNbbR57APEeTnkUeL2IbAeuAzoID6d8TFVPx/UcszZpp4cmO20JzUoUJJqu3Jq1hMaYqpKJZkNl1No1V8Ld5bS5rXaHhsa+WFZOXiyBqVKpru7KdcO0jZ5aCbdC09Jg27aNqSpuhcb2n6zIpLPk1LepdoeG2uGUCZN2lpwac5bQrIQtORlTxTJRZSErltCshLvk1NdZu1/bVpXQiMivi0jfah8qIm8Vke9a7ceb1XO3bTfm7B/9ShSIlpysQmNMlXGXnLDDd5dLdW5Cs7UrYQkN8G7gRRH5LRG5eTkfICIdIvI9IvJ14E+A7qU+xsQvtWkTlHfWNxUKSLHoOaLaMaeHxio0xlQXJ6HJWkKzbNMloUT4PSErJTpaa/eHtdX20OwDfg74CPARETkJPAg8ApwFhoBGwqTlEHAL8CqgAXgWeLOq/s3aQjerIakUqU2bKA4NARBMTFBst5kqy+EuObU12rZtY6pK1kloxBKa5XL7Z1rSShDUbifKag+nHAI+KiK/BHwv8H7gu8q/5p9sJUCRcPjebwJ/qaql1QZs1i7V3VVJaGRkBCyhWZY5S07Z2v0pxpi65FRoGsQqz8s14Sw3tdfwsQewxl1OqnqS8GDKnxSRw4RD9HYRVmamgH7gSeDLqjq6xlhNTDJbtpA7+iIAwcgI7NzpOaLqV6RIScI8XFRozDR6jsgYM0fGKjSrMe5UaDoba7c6A/HOoXkaeDquz2fWT7pnS+U6MzaGjaBamludyZBh3gkfxhjf3F1OQQnREiq1/Q16I4wXoj+j7ubaPccJbNt2IqW3uAmNHVC5HEWiEnZKavsfvTF1SQRSztj+ku3iXI4xp0LTU8NTgsESmkRK9/RUrrMTEx4jqR0loravFJbQGFOVgkx0XbRlp+Vwl5x622t7Kd0SmgRyKzSNdkDlsrgJTWD/bIypTqmoi0LUEprlGC9ECc3WGp4SDJbQJNKchMYOqFyWotiSkzFVz6nQiC05LcuYs8tpe3dtz9eyhCaB3ISmeXraYyS1w5acjKkBKTehsa3by+FWaHZtru0RHpbQJFC6Z3PluiWXg5KNBVrKnITGKjTGVCcnobGm4KXlSkJOwzQghbK1u8NzRGtjCU0CBQ0NBB3hX9wASFlj8JIsoTGmBjhLToFahWYp485yU1umRDabXeTu6mcJTUJlnGWnYHjYYyS1wZacjKkB7pKTJTRLGnOWmzpqO5cBYhysByAiNwI3AZ2w4Fd9VdWfi/OZZnXSW7Yw88ILAKRGRsjbtOBFWYXGmBrgVmiwhGYp7pbtrqba/7oWS0IjIu3AnwL3AIuNUFXCQy2NZ+4smtSInUqxlDmD9axCY0x1crdtl2zb9lLchuDu5ljrG17E9V/wK8C9wJeBzwAnwc5vr2bp3t7KdWZszGMktceOPTCmStlRBysyNmeoXm1PCYb4Epq3AF8H7rGTtGtDZuvWynWjJTTGmHqj6juCqjeSjxKa7Z21PVQP4msK7gC+YMlM7chs31a5bp60XU7GmDpgScyKjDoVmt2b2zxGEo+4EpoXgN4l7zJVw63QtEzatGBjTH2x1GZpI04Pzd7e2p5BA/ElNJ8GvlVEtsf0+cw6S/dFCU3r9LT9ZGOMMQmSL8FkuUIjKLu3dHqOaO3i6qH5G8Km4AdF5GeBR4EFh5uo6omYnmnWINXaQtDeTml0lLQqqfFxim21X3I0xiSZ/WC2XG5DcHu6REtzk8do4hFXQnOc8G+SAL+zyH0a4zPNGmW2bWNmNNyynRoctIRmEbLoNAJjTPWxf7OLGSlE34q7Gj0GEqO4kovfxVLjmpPZupWZ554DID00RG73bs8R1Qa1v+rGVCdbOl+2UWeH0+bm+pitFUtCo6rvj+PzmI2V2RbtdErb8QfGmHpi86IW5TYE97XVwbkH2FlOiZbZFjUGN4zaLJrlsgqNMabWjToJzbZN9bHmFHs/i4jsAK4DNgEjwNdV9VTczzFrN2e43rglNItxe2jUytrGVCcbhbZs7gyanV2tHiOJT2wJjYjsAv4b8LoF3vcPwPeq6vG4nmfWLu0kNM0Tkx4jqX6BU8ws2im+xlQn5/wmdQ6qNK806jQF18MMGojvcMo+4EFgO+GOpy8BZ4GtwB3A64GviMiNqnoujmeatXN7aNqmbLjeYuYkNHaKrzHVqZiPLu0Q2UtSndtDs29rl8do4hNXheanCZOZHwP+o2r0I6yIpICPA78M/BTw0ZieadYovXkzpNNQKNBUKCAzM2hD7R9Qth7cE7atQmNMlSrmKpcaWEJzKRPFgKKGy+iNQYktne2eI4pHXE3B/wr4e1X9FTeZAVDVoqr+KvD3wJtjep6JgaRSZLdHw53TA4Meo6lucxIaq9AYU52cCo0tOV3akLPc1N2gBEF97A+K67+ij3A68GIeLd9nqkhm167KdfriBY+RVLdAo38qBS0scqcxxhunQlMSm+F6KcPODJrelvpIZiC+hGYEWGoq267yfaaKZHfuqFxnBq1CcynWFGxMDSg5FRpLaC5pKB/92Wxtr48ZNBBfQvMV4O0icttC7xSRm4F3lO8zVSSzY2flunHE8s1LsSUnY2qAs+RUCiyhuZRhZ8lpV2ezx0jiFdf/8f9A2EfzgIj8AfAFwl1OfcDdwHcBJeDnY3qeiUl2V5TQNNtwvUuyXU7G1ABnyQnrobkkd8npst76OcMvrqMPvi4ibwfuA94NvMt5twCDwAdVdak+G7PBMjujhKZ1YsJjJNXNKjTGVDnVOXNosArNJblNwQfqZMs2xDhYT1X/UkR2A28Brgc6CHtmHgP+TFXtu2UVymyPemjap6agVII66XiPk5vQlGwaqTHVx1luymtAkLJt2wvJlYSJ8pTgAGXfNktoFlROWn6v/MvUgFRrC6nubooDA6RUyYyOkt+0yXdYVWfOkpMUKWmJQCzxM6ZqFKajS7WDKS9l2BmotylTpK2lxWM08bKvyIbsjqhKE1y46DGS6iUIaY3y/8mcHRVhTFXJR/8mc2rLTZcy7Oxw2txUX4nfqv6vi8h7y5efU9Ux5/WSVPV3V/NMs34yu3Yx9cQT4fXAADMH9nuOqDqlSVMgXKOfyE3Q2lAfB7oZUxdyUVfDTMkSmktxG4K3tdVX4/Rq/6/fByjwEDDmvF6MlO+xhKbKuLNoskNDHiOpbhkyTBOWtcemx+ht6/UckTGmwq3QxNtNUVfchuAdnY0eI4nfav+vf5AwOTlbfv2BeMIxPrizaJpGbRbNpWQ0E6blwPjMuN9gjDFz5WzJaTncJac9PfWzZRtWmdCo6n3zXn82lmiMF+4smlabRXNJaeefiyU0xlSZfLTklKO+llLiNOQ0BR/oq68NILE0BYvIXSKya4l7dorIXXE8z8Qru2dP5bpjcjKc52BeIeN8kbSExpgq4/TQWIVmYUWdW6G5YmePx2jiF9cupy8A71/inveW7zNVJtXdTdAaNrg2FIukxu2b9UIyGiU0Ezkbq2RMVXGXnKxCs6DhfJpSed28PV2kp7Pdc0TxiiuhWc7er9mmYFNlRITs3r2V15n+fo/RVC93yckSGmOqjLPklBdLaBYy6FRnepvCr/31ZCPn0Owi3BFlqlB2757Kdab/grc4qpm75GQJjTFVxqnQ5KmfE6TjNOAkNNva6y/pW/VCo4h8ct6b7r5EtpciTGbeiZ22XbXcPpqGgQHLPBfgJjSTeRusZ0xVcf5NFqxCsyC3QrO3u8ljJOtjLZ1Tn3KulfBU7bsXuf808ONreJ5ZRw3OklPLyDA2L/iV3B6a8bz1GRlTVXLRv8l80OAxkOrlVmj299ZX/wysLaG5p/y7APcTDtdbaPt2ERgAvqlqp/pVK7eHpn3M6jMLaSD6IjmWsz8jY6rK1HDlckbqr/oQB7dCc8WObo+RrI9VJzSq+sDstYh8lvBE7QcW+RBTxbK7ol337ZNTSLGI2mm1czRolNBYhcaYKjMdDQXNp5o9BlKdpp1TtlMoh3Zu8RxR/GJpClbVD6jqn8fxuYwfQXMz6a194TWQsSMQXsGt0EwUrCnYmKriJDS5wBKa+QZzUf2iK1ukpbn+qlh22rapcPtoUufOeYykOs2p0BSsQmNMVZmOlpzyaUto5nOXm7a21ue3/tj+q0Rkq4h8WkSOisiUiBQX+FWI63kmfu5Op+wFawuez63QTBZtl5MxVcWWnBblNgTv7KjPpulY5kOLyHbgYaAXeBpoAF4GZoDLys95HLCTD6tYdk9UoWkaGrT/WfO4FZqp0pTHSIwxr+AkNIV067KmvSaJW6G5bEurx0jWT1wVmk8CfcAbVPWa8ts+o6qHCBOavwOagLfF9DyzDtydTq0jls7M51ZoptQSGmOqhuqcXU7FTH1+w14Lt0JzaFunx0jWT1wJzbcAf6uq/zj/Hap6CngHYULzszE9z6yDhsuihGbT2LgdUjlP1pk+OqMzlGwKgTHVITcBWgRgppQiyDR6Dqi6lBQG8tEcrat319ehlLPiSmj6CJeaZhUJExgAVHUc+AfgLTE9z6yD9LZtSHO49txUKNghlfOkSFWG66moHX9gTLVwlpsmSxmCoD6bXldruJCiqOEiXEuqyI4tXZ4jWh9x/V8fhTmHZwwB2+fdMwLUZ1pYJ0SEhv37K68zttPpFdxlp4vj1jhtTFVwdjhNqp3jNN+FXFSd2dZM3SZ8cf1XvQzsdF4/AdwrIs0AIhIArwdOxfQ8s07chCZ77rzHSKqT2xh8YcwO8TSmKkxFc7OmLaF5hYvODJpdm+r3zyeuhOafgHtEKieCfRbYBvyziPwK8CBwGPjDmJ5n1omb0DQPWAVivqZoJZULE5bQGFMVJqKvVePU38C4tXIrNPu3tHiMZH3Fsm0b+O+Ey0ybgbOq+r9E5AbgY8CR8j1/APyHmJ5n1knDgSihaRsaxhad5mpSJ6EZt4TGmKowGSU0k5bQvMJFpyH48Pb63OEEMSU0qvoC8Evz3vZxEfl5wm3bx1XV1i9qgFuh2TQ2Fu50EpvoMMtNaC5OWQXLmKrgVGgmpX4rEKtRUhhwlpyu3dvrMZr1FVeFZkGqegGwH2NrSLqvD2lpQScmaCwUSI+PU2hr8x1W1XCXnAanBj1GYoypcBKaqcBm0LiG8mmK5TGDrakiO3rr75TtWfXZ6mxWLdzptK/y2nY6zeVWaIZm7ABPY6qCs+Q0k7KExnXRPcOpjnc4QYwVGhHpAj4I3AR0AqkFblNVfU1czzTro2H/fqafeBIIE5qpAwc8R1Q93ArNSM6mKRtTFZwKzXTKKsoutyF4dx3vcIL4znI6BHyRcM7MYg0XNnq2BjTsjxKY5osDjHqMpdq4FZqRgiU0xlQFJ6HJZdo9BlJ93C3bB3rru3oVV+3pV4EthI3BlwEZVQ0W+LVQ1cZUGbcxuG3YllVczUSn+I4XbJKyMVXBGaGQz3R4DKT6XEjIDieIb8npTuCvVPUnYvp8xiN363blTCfb6QTMrdCMqyU0xnhXKoHToF9s2LRgv0MSlRQG3R1Ol/V5jGb9xVWhEeCZmD6X8Szd20tQ3tnUWCiQHrVFp1kNNBBo+M8mR46Z4ozniIxJuKkhKB8UO17MEGQalviA5Bhwdji1p4tsr9MznGbFldA8ChyM6XMZz0SEhoOXV15nTp/2GE11EWROY/DZkbMeozHGMNFfuRwvNSBWTa7odxqCd7RK3f/ZxJXQ/DvgTSJyd0yfz3jWePBQdH3Wtm67mjXqozk9bMmeMV6NnqlcjpSaF7kxefpnooRmX3f9V67i6qHZCXwe+HsR+X3Cis3wQjeq6u/G9EyzjhoORQW31gsXsNbgSKu2cqE8L/LUiJ23aoxXY9EPXKPU9y6elTrvVGiu2Fr/u7/iSmjuI9ySLcB7yr/mb9GW8tssoakBjYeiCk3H8DAnPcZSbVqIRqufG7PqlTFejUUVmnGxhMblJjTX7unxGMnGiCuh+UBMn8dUiYYDByAIoFRi0+QkQT5PKZNZ+gMToEWjhOb8hB1RZoxXzg8VE0H9VyGWa6IYMFEM93ulpcQ1l23zHNH6i+twys/G8XlM9QgaG8nu3UvuxRcRIHv2LNO7dvkOqyq0avRT4IUpO6rMGK9Go8b8ybTNoJnl9s/0NZZoaa7/U8jr91AHs2aNB6M+muyZM4vcmSxuhWYgN+AxEmOMu+Q0ld7kMZDq4i437dm0rudQVw1LaMwlNTh9NE3nbWlllttDM5xfsPfdGLNRnCWnXEP9niS9Um5Cc3BLMnqLVpW2ichLhA2+r1XVY+XXy6Gqum/p20w1aHR2OrUPDmIpTcit0IyU7DwnY7wpFmA8+sqUb+yO78TlGucuOR3ZVd8D9WattkITzPvYgHAX01K/rCJUQ9wKTdfoWHgEgqGRRlLlY8ly5JjIT3iOyJiEmrhQmRI8WsySytZ/n8hyFDScEjzrxv1bPUazcVaVzKrqnsVem/qQ7ukh1dVFcXCQbLFIZnCQfLeVdAWhhRZGy+eQnxw8yaHeQ0t8lDEmdk7/zHCxqe4n4S7XxVyGUvnIg85MgW1bkvF12yom5pJEZM6yU+aUTcWd5S47vTz0ssdIjEkwZ0rwqPNvMuncIw92tgaJSfQsoTGLanCOQGg6Z+cWzWrXaN7FiaETHiMxJsGGo5GfI9gMmlnnnP6Z/T3JWYZbbVPwe1f7QDv6oLY0Xnll5brtwgVsk3KoTdsq16fG7PgDY7wYiRKasZRt2Z7lJjRHdnZ6jGRjrbYh/D5eebTBUuzogxrUeNXhynX30DDHVSEh5cvFuAnN2QmrXBnjxXBUHR1PJ2Mnz1JKOnfL9s0HktEQDKtPaOyog4TI7t6NtLSgExM05/NkRkfJd9g0TnfJqX+632MkxiSYk9BMZJLR+LqUgXyavIbdJK2pIpfv7PUc0cZZ7S4nO+ogISQIaDp8mMmHHwYge/KUJTRAG1GFZiBvC3HGeOEkNNMNPVjteO5y0642SKVSHqPZWNYUbJbUeDhadmo8bTudYO6S04iOUCgVPEZjTAJNj8J0OKk7VwooNlmFBuDsTLZyfTBBDcEQU0IjIjeIyCdFZMHaloj0ld9/bRzPMxvL7aNpv2DLKwBp0jRrMwCKcmbUzroyZkM5DcEDxWbSmewiNyeHW6G5JkENwRBfheZHgA8Dl/pudx74EPDDMT3PbKAmp0LTNTRsE4PL3D6aFy++6DESYxLIWW4aKiXjrKKlzG8IvilBDcEQX0JzK/AF1YW/05Xffj9we0zPMxsos2sXQVv4BaM5nyczYucXwdxlp5cHbbieMRvKmUEzbDNoALjoNAS3pYoc3NXnOaKNFVdC0wcsNYzjDJCsdLFOSBDQeGVUpcmePLnI3cnhJjQnRmy4njEbajj6IWI0sBk0AOec/pmkNQRDfAnNJNCzxD09wExMzzMbzO2jaTpj/SIwd8np9Lg1SxuzoeZs2bYZNABnnf6ZpDUEQ3wJzePAW0RkwYVMEWkH3lK+z9Qgt4+mrf+Cx0iqR4dG29fPTZ/zGIkxCTR4rHI5kV3q5+lkmNMQvCt5SV5cCc1/I6zA/IOIHHHfISLXAH8PbC7fZ2pQ41VXVa67h4asMZi5CU1/3nZ/GbNhVGHwpcrLyUbrZpjfEHzL5ds8RuNHLAmNqv4h4ZEGNwOPicgZEfmaiJwBvg7cBPyuqv5+HM8zGy+zcydBW9gz0lQokBm2xuA22gjKDXjjOs5EfsJzRMYkxPh5KP97myhmoCl51Yj5LubTFGYbgtNFDiRoQvCs2Abrqer7ge8FniFsEr6h/PvTwEdU1Y5LqGEiQtPVUZUm+/Jxf8FUiYBgTh/N0QtHPUZjTIIMRGMS+outBAlrfl3ImemoIXhPmxAEyZubG+t/sar+N1W9GmgFdgCtqnpEVX8nzucYPxqvuaZy3XzKmmABNmm0u+K5/uc8RmJMggxGCc1AyY5iATjt7HC6qq/FYyT+rPZwykWp6iThzidTR5qORO1Rnf39WGvw3ITmJWdN3xizjpx/a4OBLTcBnHYqNK+6bLPHSPyJNaERkR7gO4ArgBZV/bDz9r3AU6o6FeczzcZpcio03SMjSKGAptclJ64ZbmPwy6M2XM+YDeEsOY2mk/nN2zVdEi7mw6/FgnLroR2eI/IjtiUnEfkQcBz4NPAxwO2Z6QX+BXhXXM8zGy/d1UVm587wWpWGs7ZV2a3QnJmy+TzGbAinQjOe3eIxkOpwdjoL5bPG+xqKbO1JZtUqrsMpX0e4Jft54K3Ab7nvV9VvEDYHf3sczzP+NF0bnS/a+LJVJNyExrZuG7MB5m3ZnmpK3vbk+dz+mQPdya2ax1Wh+THgLPBqVf1zFj6k8kngypieZzxxl51abWIwrbRWtm5P6ATjuXHPERlT58bOQT5s0RwvZpCWbs8B+XfGSWiObE9uk3RcCc2NwF+q6ugi95wi3MZtapib0HQNDHiMpDoEBHP6aL7Z/02P0RiTAM4OpwvF1kRuT3apwunpaKDerQeSN39mVlx/E7LAUlPFNgHFmJ5nPGk8eDnS0ABAx9QU6XGrSLjLTs+ef9ZjJMYkwMXno0vt9BhIdRgqpJgqhXN4GoMi1x/Y6Tkif+JKaI4TDtJbzM2A/fha4ySbpdE51ylrfTR0adSA9/zA84vcaYxZswvRt5GLge1wcgfq7W5VmpoaPUbjV1wJzeeBO0XkHQu9U0Q+ABwB/k9MzzMeuctOzSdPeYykOrgJzbHRY4vcaYxZswvRAMuRjHUxuA3BV2xp9hiJf3G1Q/8y8E7g90Xk7UAHgIh8FLgTeBvwAvDrMT3PeNR0TTRgr+P8eS56jKUauAnN6WmboGzMunIqNGNNyZy34nIH6t24N9kN0rEkNKo6JCKvJjyg0q3S/Jfy718G3qWqdnpfHXArNJuHh3mxVIIEN+Z1Ouv4F4sXyRVzZFPZRT7CGLMqU8MwdhaAvAbkmvvILPEh9Sxfgn7nhO07r0xu/wzEOClYVU8Ad4vIEeBWoBsYAR5S1Ufjeo7xL93XR7q3l8L582SLRRrOnWNmW3JnQWTI0FZqYywYQ1GODhzlyi02ocCY2DkNwWfzbWQamjwG49+ZmSyl8kC9zdkCu/qS3VMU+4/Vqvqkqv7/qvrzqvppS2bqj4jQfMP1ldeNx6xvxF12+sbZb3iMxJg65vTP9Jc2LXJjMpxylpsOdacREY/R+BdrQiMiu0XkRhG5QUR2xfm5TXVpulSX9D4AACAASURBVD7a1NZuJ2/PSWieu2CnbhuzLpz+mYGgx2Mg1eHkdEPl+rqdyR2oN2vNCY2IbBaR/ygiZ4GXgK8CDwPHROSMiPyKiCTzYIk61nxjlND0XLgQTndKMNvpZMwGcBKaoUxyB8gBlHRuhebVV2z3GE11WFNCIyIHgEeAHyQ8gLJIeOzBhfJ1H/DDwCMictnaQjXVpOHAAaS1FYCWXI7s0JDniPxyE5pTk7aV3Zh14SQ0443J/gben8uQKx+70poqcs1+2/G16oRGRALgfwO7gAeA1wKtqrpVVfuANuD1wJeAPcD/WnO0pmpIKkXzdddVXje8lOyqhJvQ9Bf7yZfyHqMxpg7NjMPICQAKKuRak/0N/KRTndnfAZlMkvd7hdZSoXk94RlOfwS8RlXvV9Xc7DtVdUZV/xG4F/gT4ObyqdymTjTfEC07tZ486TES/7JkadWwYlWixAsXX/AckTF1pj86VuR8vpV0wnc4uctN125v8xhJ9VhLQvMdwAzwMdVLN1CU3/dRIA+8fQ3PM1XG3enU3b/QAevJ0l2Khlo9duoxj5EYU4fOP1W5PKvJHiCnOrch+PbLbWIyrC2huR54UFUvLHWjqvYDXyl/jKkTjUeOQLnM2TkxQWZy0nNEfvVotOvi6QtPe4zEmDp0LhqH0B8kuyF4uJBivBgeSJmVErdeudtzRNVhLQnNTmAlX7WfBuxPvY4EDQ00XXVV5XU24X00mzUaavXiyIseIzGmDp2PEpqhbLIbgt3lpj2tJVpbkn2G06y1JDTtwPAK7h8mbBQ2dcRddmpJ+MnbbkJzYvqEx0iMqTOlEpyPfn4ebUr2mDN3uenIVktmZq0lockSbs1erlL5Y0wdaXIagzvPnfMYiX8d2kFaw9NExnWci5NJP7bTmJgMH4fcOACjxSy0JnvJyd3hdMv+LR4jqS5rHayX7GlqZs7W7e7RUYJcbpG761tAQLfTrPj4mcc9RmNMHTkXNQSfKnSSSsd2DGHNmSgGDOTD3sUA5dVXWSfHrLUmNJ8SkeJyfgGfjCNgU11SmzbRcPnl4bUqjceO+w3IM3fZ6YkzT3iMxJg64jQEnyfZRx6cmIqqMzuai/R02ZlWs9aa0MgKf5k61HzTTZXrlmMveYzEv82lKKH55uA3F7nTGLNsTkPwQGarx0D8e9ntn+lr9BhJ9Vl1QqOqwSp+peIM3lSHllturlx3nTnjMRL/3ArNsYlk7/oyJjZOhWakMdkNwS9POfNn9ie7WjVfrKdtm2RqftWroHxs/ebhEVIzM54j8sdNaPoL/eSKye0pMiYWU8NzjjyYaUtuQjNeiPpnUiivuWav54iqiyU0Zs1SHR00HDoEhH+hmhLcR5MlS3upHQiPQPiG85OlMWYVzj1ZuTydbyfdkNxtyu5y086WIlu6Oz1GU30soTGxaLk5WnZqfinZfTRbNNpG+fDJhz1GYkwdOBMdI3K6lOwtyu5y0zXWP/MKiUtoRKRbRD4sIp8TkaMiMiUiIyLyFRH5UPkU8YU+7jYR+WsRGRSRSRF5UkR+SESsLwhovjlqDO5OeB9Nr0YzMr7RbxUaY9bk9Ncrl/3pbR4D8c9NaO64PNmzeBaSxM387wB+CzgLfAE4AfQCbwN+B3ijiLzDPXBTRN4C/B9gGvhDYBD4VuA/AbeXP2eiNd94IwQBlEp0j46Snp6m0JjMnyC2OD9FvjBmp24bsyZOhWagcY+/ODwbLQQMFcJv2WlK3HP1Hr8BVaHEVWiA54FvA3ao6rtV9d+q6geBQ8BJwlPE3zZ7s4i0A79NOBX5blX9kKp+ArgW+Bfg7SLyzo3+j6g2qbY2Gg8fBsL9+Y0JXnbaolsqIyfPFs4yVZjyG5AxtWpyEIbDI1XyGjDVtsdvPB651ZndrSU22/yZV0hcQqOq96vqX6hqad7bzwH/tfzybuddbwd6gD9Q1Uec+6eBnyq//L71i7h2tDjLTi0JPqgyS5ZODZv1FOXJs08u8RHGmAU51ZmTuQ6yTa0eg/HLTWiutfObFpS4hGYJ+fLvBedt95Z//9sF7v8SMAncJiINC7w/UZqdxuDus2c9RuKf2xj8tZNf8xiJMTXsTNQ/c1oT3hDs7HC686D1zywkiT00CxKRNPDe8ks3eTlY/v35+R+jqgUROQYcBi4Dnl3iGY9e4l2HVhZtdWq+/npIpaBYpHtsjNTkJMXmZP4ksUW38E3CScFPXXhqibuNMQtyzkPrT2/3GIhfw/kUI+X+mYyUuOeayzxHVJ2sQhP5ReAq4K9V9e+ct3eUfx+5xMfNvj3xC5pBSwtNR45UXjcdPeoxGr96S9FPUEfHkvvnYMyaOEtOQ83J/SZ+3Flu2ttWoqMtuUtvi7GEBhCRHwB+BHgOeM9KP7z8+5Inj6vqDQv9Kj+3LrTcemvlui3BjcGbdTOi4V+N/mI/E/kJzxEZU2PGzsPoaQBmSqlETwg+5iQ0N+6wZOZSEp/QiMj3A78GPAPco6qD826ZrcB0sLD2efclWssdt1eut5w5C7pknleXMmTo0q7K60dOPrLI3caYV3CqMy/nO8k0NHkMxp+SwvGpaATGaw4nd+ltKYlOaETkh4DfAL5BmMycW+C22SOTL1/g49PAXsIm4uSWIxxNV1+NtLYA0D49TcPg/PwwOdwBezYx2JgVOhU1058luU2w53MZpkrht+qWoMgdV9n5TZeS2IRGRH6McDDe44TJTP8lbr2//PsbFnjfXUAz8M+qmtwTGR2SydBy8y2V183Pv6KXOjH6Sn2V6ycuPOExEmNq0MmvVi7PZXZ7DMSvlyaj5aYruoSGhsRvqL2kRCY0IvLThE3AjwKvUdWLi9z+J8BF4J0icqPzORqBf19++VvrFWstarn9tsp1R4IPqtyqWyvXRyePogldfjNmxYqFOUceDLUe8BiMX8ec5abb9iZ+78miErdtW0TeB/w7wsm/XwZ+QETm33ZcVe8DUNVREfl/CBObL4rIHxAeffBthFu6/4TwOART1nr77ZwvX/deuMDLxSKaSt6RV53aSVaz5CTHhE5wfOQ4ezdZudiYJfU/DeVG+oFCE7Qn8wynXEk4NZ2tvP6Wa/f4C6YGJC6hIex5AUgBP3SJex4A7pt9oap/JiKvBn6S8GiERuAo8MPAf1H70XuOzK5dpHdsp3DqNNlikeaTJ5nYs8d3WBtOELaWtvJyKhzd/uCxB9l7nSU0xizJ6Tk7VthCECRyMYET01lK5Y20vdk8V+y1huDFJO5viap+SlVliV93L/BxD6rqm1S1U1WbVPVqVf1Pqlr08J9R1USE1tui3U7Nzyf3gEZ32emRM7bTyZhlcfpnTgc7PAbi10uT0XLTkd5sYhO75bI/HbMuWm6PEprukyc9RuKX2xj87PCig6SNMbOcCs1AU3IH6rnzZ15txx0syRIasy5abrkZyj9NbB4ZIT2VzBOne7W3MmDvTOEM47lxzxEZU+XGzlVO2J4ppZhs3+c5ID9GCikG8hkA0pR4/XXJTeyWyxIasy5SHR00Xn01EI5SbnwhmeP/s2Tp1u7K66+e+Ooidxtj3OrM8Xwn2aYWj8H4c2xy7nEHW7o7PUZTGyyhMeum1Vl2an8xmQkNzO2jeejEQx4jMaYGOP0zp0jm7iaAl+y4gxWzhMasm5Y77qhc950+k9hjEOYM2LtoA/aMWZRToelv2OMvDo+KCsechuDXX53cxuiVsITGrJuma44QbAoHQbXkcjSdW+hkifq3teQM2Js6Sr6U9xiNMVUsNwFn3IF6Bz0G48+p6SwzGn57bk8XuONq659ZDktozLqRVIrWO++svG55tm4OFV+RdtppLYUl4zz5/8vefYfHUd1t479ne9GuerWaezfuHTAl2BTTWyCEBJ4QSEghveeXhCRvHpLnSXmTN4GEnmBCx4AJBgMG94Z7t+UiuUhW1/aZ8/tjxewKbMuANGd35v5cF5fnjHak21hefX0qNh3dJDkRUYY6tBrQEgCAw7EA7IFiyYHk2JvWO3NWsQNOp1NimuzBgob6Vc455+jXhQfq5AWRSIGCASK1IdZbe9+SF4Yokx1Ypl/u0ypwkl3cLWFPWkEzZ1iRxCTZhQUN9aucs2fry7eLW1rhDIUkJ5JjgJYqaNYdWycxCVEGq0sVNA1Oaw6ztMbtaOperm2HhksmD5GcKHuwoKF+Zc/Lg3f8eADJ5du+nTvlBpIkvaDZ1bULqsYNpol6iIeB+tRu2s2BERLDyJPeOzM4oKK8uPA0r6Z0LGio3+Wce65+nbvHmsu3c5ELv5bcTyOKKLY0bpGciCjDHF4DqDEAQH0sAFuwrJcHzCl9/syMmqDEJNmHBQ31u5w5qYKm9MhRQNMkppHjQ/No9rwlLwxRJqpLnz9Tbslzi+KaggOR1P4zl06okZgm+1jvO4YM5x42DPbS5DkknkQCvoPWPNspfdhpzdE1EpMQZaAD6fNnrHkq/YGIC4nuo1KKXHFMGlErN1CWYUFD/U5RFATShp1ydlpz+XZ6D83Ozp2cR0P0vnik54GUOZw/M6HUBbvdLjFN9mFBQ4ZIH3YqPnBQYhJ58kQefMIHAIgggm2N2yQnIsoQ9esANQoAOBLLgS3XekceCNGzoLlwVPlpXk0nw4KGDOGfPh1wuQAABZ2dcLW0SE5kPAVKj2GnJbuXSExDlEH2L9UvrTp/pjHmQHvCAQBwKRrmTR4qOVH2sd53DUlh8/ngnzFdb/u3WbN3olJLncmy4sgKiUmIMsi+N/XLw67BEoPIszPk1a9HFwjkBngg5UfFgoYME7jgAv26aM9eiUnkqdaq9eudoZ2IdS9TJbKsSBtwOLn/jCaAE4ExkgPJsasrNdx03lDuPfNxsKAhwwTOOw/o3sq85MQJOMJhyYmMF0QQuVouACCBBFYdXiU5EZFkde8CIjlB/mAsD/ZgieRAxmuL23EslhySt0HgiqncHfjjYEFDhnEUF+u7BtsA5GzfLjeQJFWiSr9esofzaMji9r2lX+4VlZY8v2lX2mTgIYEEaipKJabJXixoyFCBC1PDTnm7dktMIk+Vlipo1hznfjRkcXtT82fqPcMkBpEnfbjp7IG5EpNkNxY0ZKj0eTRlR4/CFo9LTCNHlVYFpXvzrAOxA2iLtklORCRJ22HgRPIfNjHNhva80ZIDGS+sKjiYtjvwFVOseShnX2BBQ4Zy1dbCNTi5isGpacix4ORgN9woEal5Akv2ctiJLCqtd2Z3rBgun/XOLtoT8kAg+Q+cSk8cYwZX9fIEnQoLGjJc4MIL9evgDmvOo0lf7fT2/rclJiGSKG259n7FmucW7epKLdeeUe2z5B48fYX/58hwgQvO16/LDtdb8rDK9Hk0G1o2SExCJImm9ZgQfNQ/Sl4WSeIasC+cGm66jIdRfiIsaMhwnjFjYC8uBgB443H4D1rvKIQyUQaHSO4K2qw2Y1/LPsmJiAx2dBMQOgEAaFddiOZZb6lyXdiDuEj+GC50JjBrrDU3FewrLGjIcIrN1mO1U2DLVolp5LDD3mPX4EU7FklMQyTB7sX65Y54BZwu92lebE4701Y3TalwweFwSEyT/VjQkBTp82jKDxxInsxmMbVarX699PDSU7+QyIx2/0e/rHNab7m2KoBdaccdXHpW5WleTWeCBQ1J4Z82Dba85H4LOdEofIcPS05kvPSCZmdoJ0LxkLwwREbqako77kBBY+44yYGMVxd2I6IlfwQHHQlcNMl6RV1fY0FDUigOB4Kf+pTeDm7eLDGNHAEEUKglz2xRoeKt/W/JDURklD2vA0j2yu6N5sMRsN5xB9s7U70zU8uccLutN+TW11jQkDSBefP06/L9dZYfdnptz2vyghAZaXfqe323Mshyxx18cLhp/vgBEtOYBwsaksY/bRpsualhJ78Fh51qtNQyzbUn1kJYsKgji1ET3T00SfV+652u3WO4yZ7A3MnDJScyBxY0JI3icCB40UV6O7h5i8Q0cpSLcrhFsqu5TWvDtqZtkhMR9bPDq4FI8riP5oQHsbyhkgMZL324aUqZAx6P5zSvpjPFgoakCsybq1+X7d9vuWEnG2w9dg3m8m0yvbThpm3xSjhdLolhjMfhpv7Dgoak4rBTz3k07za8Ky8IkRF2pQqag+4REoPIweGm/sOChqT64LBTwIKrnWq0mvcXfGBfZB9aIi1yAxH1l9ZDwPHkRppxYUNLvvWWa/cYbip3wOv1nubV9FGwoCHpghenVjtVWHC1kxdelIkyAICAwMvbX5aciKif7Eh9b++KFsPpz5cYxngfHG66fDxP1u5LLGhIOt/UqbDl5QEA/NEo/IcOSU5kvMFa6gyX1/Zz+TaZ1I6X9MtddusNtez/wHDTvCnW+3/Qn1jQkHQfHHbK3bhJYho5BqmD9OvNHZu5azCZT9cJ4MAyAIAmgCPBCZIDGW9rp0+/nlbBzfT6Ggsaygi58y/Tryvq6qCoqsQ0xstDHgq0AgBAAgks2bdEciKiPrbrVUBoAIB90QLY86y1uiemKdiVdhjl1ZOqT/Nq+jhY0FBG8E6aBHtZch6JNx5HYM8eyYmMlz7s9PIuzqMhk0kbbtqOIZbbHXhXlwdxkfyRW+SM48JJHG7qayxoKCMoNhvy0npp8i242mmQlhp2WtuyFnEtLjENUR+KdQF7U72O9YHxEsPIkT7cdHa1F06nU2Iac2JBQxkjeNl8/br8cD3ssZjENMYrFsUIaAEAQEREsPzgcsmJiPrInteBRAQAcDgWgCgY1MsD5tKl2rAvnJovc8N0a/3+jcKChjKGZ/gwuIYmt0F3ahoC26x1DIACpUcvzcIdCyWmIepD21PDTVu1QbDb7RLDGG97pxcCySG2Km8cU0cP7uUJ+jhY0FBGyb081UtTuHWrxCRypBc0KxpXQOueREmUtRIxYNd/9OYh/1kSw8iRPtx0/qAAbDb+6O0P/L9KGSX30kv167Jjx+Hs6pKYxngVogIeLbkSol1rx7qGdZITEX1C+5cC0eRhlI1xL2IF1jruoCVuR300eV6VDQKfns3JwP2FBQ1lFGdFBbyTJwNIfnMGN1lrTxobbBgkUr00z2x9RmIaoj6w9Vn9cos6EA6LTYZN750ZFkxgxMBKiWnMjQUNZZzc+alhp+LtOyQmkWOoOlS/fufYO1A1a+3JQyaSiPaYP7PPZ63N9IQAtqSd3TRvZJHENObHgoYyTnDuRYDDAQAobm2Fp6lJciJjVYrKHsNOqxtWS05E9DHtXZI23ORDtHC05EDGOhJ1ojme7JFyKhpuPHuU5ETmxoKGMo49Lw+B8+bo7dz16+WFkcAGG4aKVC/NM1s47ERZaktquGljYpDlhps2dqSGm8YXAmVFBRLTmB8LGspIuVddrV8P2L0b0Ky12id92Ond4+8ioSUkpiH6GOJhYOcrenO/31rDTXEN2NaVKmiunVghMY01sKChjJRzztmwFRYCAPzRGIJ79kpOZKxyUQ6flnwz7BJdWH6Im+xRltm9GIh1AgCOxv2IF46UHMhYu0JeRLtP1s5zJHDFTGsNt8nAgoYykuJwIO/KK/R2wXvvSUxjPBtsGKqlemme3fbsaV5NlIHSVjdtUgdbbrhpU9pw05xqNzwez2leTX2BBQ1lrLyrU8NOFfX1cITDEtMYL72gWdG4gmc7UfaIdfXYTK8uZ5LEMMZrS9ixXz/qQODmWUOk5rEKFjSUsdyDB8MzbhwAwC4E8jZaa0+aMlGGHC0HABASIby1/y25gYjO1K5XgXgIAFAfC0AtGCY5kLE2d/iA7qMOBvsTmDSSZzcZgQUNZbT0XpqSrVskJjGeAqVHL83TW5+WmIboI9j4pH65WRsKe/c2DFYgxPsFTdKlIwt41IFB+H+ZMlrw0ksAV3Lb8MK2dniPHpOcyFgjtNQ28Wta1qCze5IlUcbqbEyert1tf3CqxDDGOxRxoSWRLODcioqbzuVkYKOwoKGMZg8EELzoIr2dt95aZxsViSIUasnVXnHE8eKOFyUnIurFlqcBkdzdelekEErBQMmBjJU+GXhyiYKy4kKJaayFBQ1lvLyrr9KvK/fug5Kw1p4s6b00z+18TmISojOwcYF+uVkZZanhloimYHtX6qiD66dUS0xjPdb5TqOs5Zs+HY6K5KZUnngcuVu3SU5krOHqcCgiOcFwR2gHGjobJCciOoXjO4AjyS0W4sKGhoJpkgMZa2uHD3GR/LFa7Irjkmk86sBILGgo4yk2G/Kvv15vl1hsTxo//KjSqvT2gk0LTvNqIonSvjc3Rirgzi2VGMZYQgDrO/x6++KhATgttveObCxoKCvkXXM1YLcDAEpPnICnsVFyImOlDzu9UvcKhBAS0xCdhKYBm/6tN7e7xksMY7z6qAuNsWQB41A03HY+JwMbjQUNZQVHcTECF16otwvWrJWYxniDtEFwiOTKiWPxY9h03Fp78lAWqHsHaK8HAHSoLrQVTZYcyFgb2lOTgScWCtQOKJOYxppY0FDWyL/xBv26cs8e2OLW2TnXCSeGaKndRv/53j8lpiE6ibTJwOtiA+Hy+k/zYnMJqwq2px1EedO0qtO8mvoLCxrKGr5p0+CoSr5RuBMJ5G3ZKjmRsUaoqWGnt469hUgiIjENUZpIG7Dteb25x2+t3pnNnT4kuiful7njuGQah5tkYEFDWUOx2VBw4416u9Rik4MrRSUCWgAAEBZhvLzrZcmJiLptflo/6uBgLIh40RjJgYwjBLChPW0y8LAAXN2bgZKxWNBQVsm9+iqge+VAUUuLpXYOVqBgtJb6l9+CbVztRBli/aP65Tox2lJHHRyKuHAinnxPcioaPn/+WMmJrIsFDWUVR35+j52DC9askZjGeCPVkak9abp2oK6tTm4goiMbe+w9c7hgluRAxtqQtlR7SrFAdXmJxDTWxoKGsk6PycH79sEesc5ckhzkoEar0duPbXhMYhoi9OidWR+pstTeM50JG7Z3pnYGvmWGtY55yDQsaCjreCdPhmtIcsWPS1VRsGGD5ETGGqOl5icsOrQIcc06q70ow8RCwKan9OZWzxSJYYy3ocMPDcke0ypvHBdN5c7AMrGgoayjKAoKPnuL3h6wcVNyUy+LqNFq4NOSS0Q7tA68se8NyYnIsra9AETbAABH436EiydIDmSchADWp00GvmZsAezdm3+SHCxoKCvlzp8PJRgEAARCIeTu3iM5kXFssGGUlvqX4D83c08akiRtuGmtOhJOC63u2dHpRZeaLGBy7AnceoG1dkbORCxoKCvZvF4U3JB2vpPFJgePUlMFzcb2jWjo4IGVZLDGncDB5QAAVSg4kG+dycBCAGvac/T2hTUu5OcGJSYigAUNZbH8T38asCW/hcuOH4e3sUlyIuPkIhdVanKTQQGBh9Y/JDkRWc6av+uXGyMVcOZXSgxjrIaoE0eiyd4oOzR84XzOnckELGgoazkrKnqc71S4aqXENMYbq6X2u3jp4EuIqTGJachSoh3Ae0/ozU2e6RLDGG9NW6p3ZmKhhtFDak7zajIKCxrKagW3fEa/rtyzF46wdZZwD9QGIkdLvrF2ap14ceeLkhORZWxcAMQ6AAD1sQC6iidKDmScjoQNO7pSS7VvnVkrLwz1wIKGspp38mS4hg8HADg1Dfnr1klOZBwbbD16aR7bwj1pyABCAKsf0JurxFhLTQZe355aql3jjWMez23KGCxoKKspioLCtCXclZs2QVFViYmMNVodDZtI/jXeF96HzY2bJSci09u/FGjaCQAIaw7UF50jOZBx4prSY6n2tWcVwWGhYx4yHQsaynrByy6DrSAfAJATiSB/2zbJiYzjhRdDtaF6++9r/36aVxP1gTVpvTORQXAHCiWGMdamTh/CWnKpdq4jgVsv5FLtTMKChrKeze1G4S2pXpry1auT3eIWMU4dp18vPb4ULZEWiWnI1FoPATtSp7xvD8yWGMZYmgBWt6YmA182xIdgTs5pniCjsaAhU8i78UbA4wEAFLS1I7h/v+RExikTZShRkwfiJZDAo+892ssTRB/TuocAkdyVe1ukGErxcMmBjLOzy4OWRHJ4yaOouGsee2cyDQsaMgVHfj7yr7tOb5euWCExjfHGaalemqf3PM3znajvxULA2tR+Rxsck2GzWeNHiBDAyraA3j6vyo7KsmKJiehkrPHdSJZQcOutqY32jh2H7+hRyYmMM1QbCq+WXEraqrZi4c6FkhOR6Wz8FxBuBgAcj/vQWjpDciDjHIy4emykd9eF3EgvE7GgIdNwVQ5AYN48vV2y3Dq9NA44cJZ2lt7+x6Z/QFhoHhH1M00FVvxZby5Tx8Hp9p7mAXNZldY7M6VYw7hhAyWmoVNhQUOmUnj7bfr1gLo6uNvaJKYx1hh1DOwiuQLjYOQgVtRbp6CjfrZzEdC8DwDQpTlxuPg8yYGM0xhzYE/I090SuHPO0NO+nuRhQUOm4h09Gr7pyW3YbQCKLNRL44W3xyncf137V4lpyFRW/F/9cllkGNyBAolhjLUqbWXT6NwEzpkwQmIaOh0WNGQ6hbffrl9X7dwJZygkMY2xxqvjge6Rpg1tG7CnZY/cQJT9Dq8FDib/YaAKBbvyrdM70xq3Y0unT2/fNrPaMhOhsxH/ZMh0/LNnwTVyJIDkcQjFy5dLTmScPJGHgVpqfP8vq/8iMQ2ZwvI/6Zerw9VwFlRLDGOsFa05+jEHtb44rpg1rpcnSCYWNGQ6iqKg+Et36e3qrdvgCIclJjLWRDV1UOCSo0vQFG6SmIayWksdsD116Okm/zlQFEVeHgN1JGzY1JE65uDzU8t4zEGGY0FDphS44AI4hwwBADhVFcUrV0lOZJxyUa5vtKdCxd/W/E1yIspay//UYyM9UTpGciDjrGgNQO3unan0xHDjeRMkJ6LesKAhU1JsNpSk9dJUbd4MeyQiMZFxFCiYpE3S28/VPYe2qHVWe1Ef6TgKrE+dpaF1BgAAIABJREFU4L7aOdMy80c6Eza8l9Y789lJJXC73RIT0ZmwxncnWVJg7lw4amsAAO5EAsWr10hOZJzB2mDka8kDO6Miin9s+IfkRJR1lv8JUKMAgH3RfITKpkkOZJxVbTlIiGTvTLk7js9+alIvT1AmYEFDpqXY7Si+8069XbVxI+yxmMRExlGgYLI6WW8/uftJhOLWWe1Fn1CouccxB8ts0+FwOiUGMk5ItWF9e6p35uYJhfB4PKd5gjIFCxoytdzLLoN9wAAAgCceR+Ea6/TSDNOGIaAmdzgNaSE8uomHVtIZWvn/gHgXAOBQLIj28lmSAxlndVsO4iL5o7HEFcdtF03u5QnKFCxoyNQUhwPFd35Rb9es3wB7NCoxkXFssGGylnozfnTbo4gkrDGPiD6BSBuwKjWR/B1MhdNljfkjXaoNa9tSvTOfPqsAPp91jnjIdixoyPTyrrgC9gEVAJK9NMWrrLPiaaQ2Ej4tuTFYh9aBBVsXSE5EGW/N34HuSeRH4340l50jOZBxVrbmINbdO1PkiuOOi6dITkQfBQsaMj3F5ULJ3V/R2zXvbYQjbI2eCjvsPVY8PbTlIcTVuMRElNFiXcCK1GaMS7XJcHms0UPRkbBhXXvqmINbJxTCz96ZrMKChiwh9/L5cNTWAgBciQRKLLR78Gh1NDxaclJjc6IZT2x5QnIiylir7wdCyY0YmxJeHC+bIzePgZa1BvSVTWXuOP5rHufOZBsWNGQJit2O0q99VW9Xb94MZ1eXxETGccLZo5fm/s33cy4NfVikDXj393rzzcQkuLw5p3nAPFrjdryXtrLptsnF8HrZO5NtWNCQZQTmzoVz2DAAyTOeSt99V3Ii44xVx8KrJd+g29Q2PLb5sV6eIMtZ+f+ASCsA4Hjcj2PlF0oOZJx3WwL6mU1Vnhhu5cqmrMSChixDsdlQes/X9Xb1tu1wt7dLTGQcJ5yYoqYmOD605SHuS0MpoWZgxZ/15hJtKlxe/2keMI+mmAOb007U/uLMCu4KnKVY0JCl5MyZA/e45Im5diFQ+vZSyYmMM0YbA7+W/CHVoXXgofce6uUJsozlfwKiyeK+IZaDpvLzJAcyztKWAER378xgfxw3ns9dgbMVCxqyFEVRUPqNe/R21e7d8DY2SkxkHDvsmKamtq9/dMej6Ih1SExEGaGzEVj1V735JqZbZmVTfcSJHV2p3pm7z63hidpZjAUNWY5/+nT4ZiV3PrUBqHxjidxABhqhjUBQDQJI7h78t3U8idvy3v1foHv48WAsiJbycyUHMoYQwBsncvX22Nw4rph9lsRE9EmxoCFLKv3Od4Duk4PLGhoQrKuTG8ggdtgxTUv10izYvQBN4SaJiUiqlgPAmgf05tvKLLjc1ji3aFfIg8PR5FwZGwS+PXe4ZU4TNyv+6ZEleYYPQ+6VV+rt6iVvApomMZFxhmnDkK+mTuL+3YrfSU5E0iz5BaAmD2zdG81HR8XZkgMZQxXAm82p3pnZZRrOmThSYiLqCyxoyLKKv/ZVoHs1Q35rKwq3bJGcyBg22DBbm623Xzn0Cva17ZOYiKSoXw9sfkpvvum8wDInam9o96M5npwr41ZUfH/+eMmJqC+woCHLcpaWouj22/R2zbJlsMWtcSxAjVaDAWryFHINGn71zq8kJyJDCQEs/oneXB+qQLzcGnuvRDQF77QE9Palg5wYObhaYiLqKyxoyNIKbrsdSkEBAMAfjqBk1WrJiYyhQMFsNdVLs+rEKqw5skZiIjLU7teAuncAAKpQsDJnHux2u+RQxljRGkBYS/5eg/YEvnvVtF6eoGzBgoYszZ7jR+lXU0ci1K5bB1dnp8RExikRJRiWGKa3f/nuL6EJa8wjsjQ10aN35p3QENhLR0gMZJyWuB2rW1PHOXxmXBClRQUSE1FfYkFDlpd37TVwDh4MAHCqKga88YbkRMaZoc6ATSTfBvaG9uLlPS9LTkT97r3HgcYdAICw5sDmwkugKIrkUMZ4/UQu1O5N9Co8cdw9f7rkRNSXWNCQ5SkOB8p//GO9Xbl3H3IOHZKYyDhBBDFeTU2I/O3q3yKcCEtMRP0q3Aq88Qu9+UZkLNwFlRIDGWdvyI3dodSGgd+cUwWfzxobCFoFCxoiAP7p05Az9yK9Xbv4dcss456sToZbS672ak404y9r/yI5EfWbt38DhJL7DjUnvKgrv0RyIGOoAlh8Ik9vTymM46pzJkhMRP2BBQ1Rt7LvfrfHMu6S996TnMgYbrgxS52ltx/f+TgOdVijh8pSjm8HVqV2hl6kzYLLn3eaB8xjdVtOj2XaP7niLG6iZ0L8EyXq5qyoQNEX79DbNcuWwxG2xvDLKG0UitViAEACCfx86c8lJ6I+JQSw6DuAUAEA2yPFaK2wxgGUHQkblqUt075yiBNjhw2UmIj6CwsaojSFt98Oe0UFAMATj6PirbfkBjKIAgVz1Dl6e2XTSrxz+B15gahvbXsB2J88WV4VCt70zIPT5ZIcyhhLmnMR6574XuSM47vXzJSciPoLCxqiNDa3G+U//IHert6+AzkNDRITGadMlGFEIrV89xfv/gJx1RobDZpaLAS89iO9+XZoKOzlYyUGMs7+sBtbO1OnaX9lVikK8nJP8wRlMxY0RB+Qc/758J2dPNNGATBw0atQVFVuKIPMUmfBqSW3vz8SPYJ/vPcPyYnoE3v3f4C25JyoDtWFrSVXWGKZdlwDXm1MzREalxfHZz41VWIi6m8saIg+QFEUlP/0p/oE4by2NpSttsYuuj74epzGff/W+3G447DERPSJHN8BvPt7vbkoPg3u3BKJgYyzrDWIlkRqIvAvrjrLMrshWxULGqKTcFUOQMlXv6K3a1etgqe1VWIi44xTx6FATe6eGhdx/OitH0EIITkVfWSaBiz8GqAlhw33RArQWDlXcihjHI85sDJtR+DrR7hx1nBOBDY7FjREp1Dw2c/COXQoAMChaah59T/J1SImZ4cdF6gXAN2/1XXN6/DyXu4gnHXWPwIcWgkgORH4Nc9lcLrckkP1PyGSQ01a947AVZ4Yvnvt7F6eIjNgQUN0CorTiQG/vBeie75BSUMDCrdtl5zKGGWiDGPV1MTRX638FdqibRIT0UfScRRY/FO9uTg0CvbyMRIDGWdDhw+Ho8nCzQaBH140CDl+v+RUZAQWNESn4R03Dvk33aS3B775JpyhkMRExpmpzoRPTa4Q6VA78Otlv5aciM7Yq98DugvQY3E/dpVfaYmJwO0JG95sTq1iurBSYO6McRITkZFY0BD1ouSee2ArSU6k9MZiqP7Pa5ITGcMFF+Zoc/T2y4dexpoj1pgcndV2/QfY+pzefAkXwJNj/h2BhQBeacxHVEv+WMt3JPDzG2ZaopCjJBY0RL2w5/gx4BepnXMr9u9H4Y4dEhMZZ7A2GAMTqcmU33vrewjFrdFDlZXCLcmJwN2Wh2oRr5p1mgfMY2OHD/vCnu6WwLfOKUNZcaHUTGQsFjREZyDn3HMRvPoqvT3o9Tfg7OqSmMg4c9Q5+t40x2PH8ZsVv5GciE5p0feAjiMAgDbVjfVFV1vizKK2hB2vn0gNNZ1TquLTF06RmIhkMP93OlEfKfv+92ErTp535InFUGuRVU85yMG56rl6+9n9z2Jlw0qJieikdrwMbFqgN19IzIErr1xiIGMIAbzcmKcfb5DviOPXN820RCFHPfFPnOgM2QMBDPh1amJs2YEDlln1NEIbgZpEjd7+/lvfR2esU2Ii6iHUDCz8ut5cGapGV7U1Dp/c0OFDXdpQ07fPKcOA0mKpmUgOFjREH0HO7FnIve46vT14yRK4Osz/g12BggvUC+DSkgcaNsWb8Kvlv5KcinQvfxPoOg4AaE14sKboOkvsitsSt+ONtKGm88o13HghjzewKhY0RB9R6Xe/C1tZGQDAHY9j0MKFyV1ZTc4PP85TU//qX3hgId4+9LbERAQA2PIssPVZvfmceh7ceWUSAxlDFcALxwsQ7x5qKnTG8X9uns2hJgvjnzzRR2TP8aPyv3+jb7hXfPQoylevlpzKGEO1oRiUGKS3f/D2D9AUbpKYyOJaD/YYaloWGohI9bmnecA83mkJoiGa7DG0QeBHF1ahtKhAciqSiQUN0cfgnzoVhXd8QW8PXLESOUePSkxkDAUKzlfPh1f1AgDa1XZ8+41vQxPm76HKOGoCeOYL+gZ6jQkfNpReb4mhpgNhF5anndV0+UAFV54zUWIiygQsaIg+ppK774ZrbHI7ebsQGPLiQthjMcmp+p8XXlykXqS3155Yi4c3PywvkFUtva/HWU3PKZfCFSiSHKr/hVUFLx4vALrPahroi+Hez8zhBnrEgobo41KcTlT9z/8A3mRvRaCzE9WvLZacyhjVohoT4hP09h83/BHbTmyTmMhiDiwHlv633nwlNA6i0vz7rry/G3CHmuyF8thU/PbasTyriQCwoCH6RFxVVaj4+c/0duWuXSjaskViIuPM0GagKJHsEVCh4uuvf527CBsh3AI8ewfQPcy3I1KEusqrLdFDsb7dj50hr97+0qQgJo0aIjERZRIWNESfUO78+QhcdpneHvr6G/A1mn+irB12XKxdDIfmAAAciRzBj97+EYQFNhuURtOA578EtB0CAHRpTiwOXAe31yc5WP9riDixOG2J9sySBL585dkSE1GmYUFD1Acqfvb/wV6T3HjOoWkY9vzzsEejklP1vzyRhznqHL29uH4x/rXtX/ICmd2y3wM7X9GbT8fPg7t40GkeMIeQasOzxwqgdc+bKXPH8ftbz7HEBGg6cyxoiPqAze9HzZ//L+BJ7lga6OjAoFcWWeJohJHaSIxMjNTb9629DxsbN0pMZFL73gKW/EJvvt41HOGaC+TlMYgmgBeP56NdTfYEuhUV9105DCWF+ZKTUaZhQUPUR9xDhqDi3nv1dtn+/Shbu1ZiIuPMUeegMJE82ViFiq8t/hqaI82SU5lIWz3w9O36vJldkUJsH3CjJTaRW9YaSDtFG7h7cgBnTxglMRFlKvP/bSAyUO5llyL3pk/r7UHvLkPw8GGJiYzhgAOXqpfCpSY3OjsRP4F7Xr8HqqZKTmYCiRjw1K1AKDkvq01149Xgp+H25fTyYPbbG3LjnZaA3v5UhYovXXmOxESUyVjQEPWx8u99D84xowEk96cZ/vwLcLe1SU7V/3KRi7naXL29/sR63LfqPomJTEAIYNF3gMNrACT3m3lSuwSeoppeHsx+TTEHnj/Wc7+Z337uPM6boVNiQUPUxxSXCzV/+hOU/OQYvycWw4hnnrXEpnu1Wi0mxyfr7X/u+iee2/2cxERZbvX9wLqH9OaLoYkQ1TMkBjJGSLXhqaOFiHaf0xS0J/CnmyYiNxjo5UmyMhY0RP3AWV6O6r/8GcKRnMgYbG3F4IUvWWKS8DRtGmoSqR6Eny//OTYc3yAxUZba8wbw6vf05qpQNRpqzL/fjCqA547loyWR/LvjgIZ751ZhzBDz90rRJ8OChqif+CZMQMUvUqtSSg8cQNXSdyQmMoYNNsxT5yE/keyhSiCBuxffjfrOesnJskjjLuCpz+uTgPdG87Gq7BY4XS7Jwfrf6ydycSCSmgR81wQfLuc5TXQGWNCcIUVRKhVFeVBRlAZFUaKKotQpivJ7RVG4dpBOKe+qK5H3uc/p7dp161BsgZ2EXXDhcvVyuFU3AKA90Y47X70TXfEuycmyQKgZeOIG/dDJ5oQXrwQ/A09OnuRg/W9tmx/r2lOTnS+p0vD1a+fIC0RZhQXNGVAUZTCAdQA+D2A1gP8FsA/A1wCsUBSlUGI8ynBl3/4WPLNm6e1hi19HXl2dvEAGCSKIy9TLoIjkEEldVx2+svgriKtxyckyWDwMPPFpoHkfACAm7HjSdiXchdWSg/W/HV0evJa2E/C4vDh+d9uFnARMZ4wFzZn5C4ASAF8VQlwphPieEOJ8JAub4QB+KTUdZTTFbkf1H34P++DBAACbEBjxwovwHzsmOVn/qxAVuCCR2vxtTeMa/HDpD3k8wsloKvDMf+knaAPAguh5sFeaf7jlUMSFF9JO0B7gieGvt82G1+s9/YNEaVjQ9EJRlEEALgJQB+DPH/jwTwF0AbhFURQe90qnZM/JwcAHH4RSXAwAcKoqRj3zrCWWc4/URmJKPHUS9KKDi/C7Nb+TmCgDCQG88i1gx0v6rWe7JiNU+ymJoYzRFHPgqaOFULt78vIdcTxwyyRUlBRJTkbZhgVN787v/vU1Ibpn6HUTQnQAWAbAB2B6b59IUZR1J/sPwIg+T00Zx1lagoEPPQjhT9a+nkgEo556Go5wWHKy/jdNm4aR8dTxCI9sfwSPbX1MYqIMs/S3wNoH9ebirhE4Nuha0+8E3JGwYcHRQkS05O/TZ0vgD1cNxajB5h9io75n7r8tfWN496+7TvHx3d2/DjMgC2U595AhqP3bXyGcTgBATns7Rv77KdgjEcnJ+pcCBedr56Mmnlp6e9/a+/DS3pdO85RFrH0IeDN1ZMbKUDV2Vt9s+rkjXaoNTxwpQnv38mynouHnF5bjnEmjJSejbMWCpnfvz1I71djA+/d7XYIghJh0sv8A7OiLoJQdfJMno/K++yC69xPJO3ECI595BjaTb7xngw0XaxejJF4CABAQ+OG7P8Rrda9JTibRe09AvHSP3twaLsGais/B5fac5qHsF1YVLDhSiKZ4srBXIPCNaUFce/5Uyckom7Gg+eTe3+WKsxzpjAXnzUX5z36mt/OPHceIZ5+DLZ6QmKr/OeHE5drlyEsk638NGr7z9nfw9qG3JSeTYMszEC98CUr3W8f+aB7eLLkNbp+5d8ONagqePFqEY7H399QR+OJZHtx5Bc9ook+GBU3v3u+ByT3Fx4MfeB3RGcm//joUfz+1E2xhQwOGvfACFNXcBzp64cU16jUIJJI/uFWo+PqbX8fyhuWSkxlo+0vAM1+A0j0t72AsFy/l3w5XwNw7QMQ1BU8dLURDNLVB4K0jHPjODeebfgdk6n8saHq3s/vXU82RGdr966nm2BCdUtGtt6Lw61/T28UHD2L48y9ASZi7p8YHH65Vr0VOIrmJWkIk8JXXv4JVR1ZJTmaAna8CT30OEMnCtT4WwPPBz8GdVyY3Vz+LaQqeOlaAgxG3fu/GIQp+csunTD/5mYzB76Levdn960WKovT4/6UoSgDALABhACs/+CDRmSi5807k33GH3i4+cAAjnnsetri5N6DLQQ6uUa+BL+EDAMREDHcuvhNLDy+VnKwfbX0OePJmQEv+2R6L+/Fs4HPwFFRKDta/opqCBUcLURdOzQ26ciBw7+cuMv3kZzIOC5peCCH2AngNQC2AL3/gwz8D4AfwqBCCe7rTx1Z6z9eRd/vtervo0CGMfOYZ05/QHUQQ16jXwJtIbqCWEAl89Y2vYvGBxZKT9YP3/gU8fRugJXvfjsf9eMp/q+l3AQ6rCp44UoTDaT0z82sEfnv7XDi6D28l6gssaM7MlwAcB/BHRVGeVxTl14qiLAFwD5JDTT+Umo6ynqIoKPvWN5H/5S/p9woajmDkU0+bfkl3HvJwnXod/Ink/jwqVHzzrW9i4d6FkpP1oTV/B56/Sz9ssiEewL9zPg9X0UDJwfpXl2rDv44U9Zgzc80g4H+/MI/FDPU5FjRnoLuXZjKAhwFMA/BNAIMB/BHADCHECXnpyCwURUHZV76Cwm+klvHmHzuGMQuehKujU2Ky/peLXFyvXo9APDlR+P0l3Y9ve1xysk9ICOCd3wEvf1O/dTCWi2cCt8FVWHOaB7Nfa9yOxxrSVzMBNw1V8Jvb2DND/YMFzRkSQhwSQnxeCFEuhHAJIWqEEF8TQjTLzkbmUnLHHSj+wff1drC5GeP+9S/4Tpi7bs5BDq7XrkdePLmkW0DgN2t+g/9e/d/Qem7SnR3UBPDSPcAbP9dv7Y3m4/m8/4Lb5HNmjkadeKShGM1p+8x8fpQD936ePTPUf1jQEGWgos9+FmW//hVE9+oPb1cXxj6xAMHDhyUn618++HCddh2K48X6vce2P4ZvvfktRNWoxGQfUawrOfl33UP6re2RYiwq+iI8Jl/NtC/kxuMNRehSk5N97dDw5Qle/OSWi7iaifoVv7uIMlT+VVeh+v6/QbiTkyldsRjGPP0Minbu7OXJ7OaBB9do16A6lposu/jQYty+6Ha0RbNgu6fO48DDlwK7XtVvreyqxutld5l+n5mN7T78+2ghYiL5o8WtqPjJOQX41g0XcJ8Z6ncsaIgyWM7s2Rj4r39C5Cb3dbRrGka+/Aqq3303OT/DpJxwYr6Yj1HRUfq9jSc24roXrsOulgze8ql+PfC3c4GGDfqtV7tGYW31F0y9A7AmgMVNuXi5KR9a9+bpAXsCv59fjVsvmSU5HVkFCxqiDOcdPRpDnnkaSmVq3kXN6jUY8fzzsEezaBjmI7LBhvNxPmZEZ+j3joSP4OaXbs7MZd0bFwAPzgM6GgAAmlDw767p2D/os6Y+mymsJveYWdOeo98rccXx8M1jcPHM8RKTkdWwoCHKAq7KSgx99hk4p6UO7yveX4ex/3oCnpYWicn6lwIFkzEZF0cvhr17TkZEi+Abb30Df1z/x8yYLKwmgFd/ADz3RaB7nk+X5sTD8UvQMuRqU28cdzzmwMP1JT02zBsVjOGZu2Zi0qjBEpORFbGgIcoS9mAQgx98EIFbbtHvBVpaMP7xf5p+Xs0QDMEN6g3wx/36vQc2P4A7/nMHmsJN8oK11QOPXAas/LN+qz4WwMOOzyJRO8e080aEADZ2+PBwfTFaEqlVS/MqVfz7axehqrxEYjqyKhY0RFlEsdtR+cMfoPTXv4LoXv7qjMcx8uVXMPi1xaY+rbtQFOIm7SaUR8v1e6uOrcLVz1+NFQ0rjA+0cxHw11nAwdTX3hCqwNP5d8FZNsL4PAaJaQoWNubj5cZ8JLon/zoVDV+Z6MGf77oUOX5/L5+BqH+woCHKQgVXXYWBTy6AKCvV71Vs2YJx//wnvCber8YDD67G1RgfHQ90z4luibXgi4u/iD+s/wPimgHnXyWiwKvfB564EQgnh/s0oWBh11lYVnUXvLnFvXyC7HUs6sSD9cXY0unT7xU64/jT5TX45vUXmHp4jTIfCxqiLOUdPRrDFy6E67zz9HuB5mZMeOxxDFi7DtAyYH5JP7DBhrNxNi6PXQ5XIrkLrYDA3zf/HTe9dBN2t+zuvy/esAG4fw6w8i/6reaEF39PXImGITebdvKvJoB3WwJ4qD61WR4ATCqI4/m7ZmDejHES0xElsaAhymL2QACD/vJnFP3oR/oQlF3TMGjpUox98t/wtLRKTth/alCDz6ifQVk0tVHdjpYduH7h9fj75r8jofXh8FsiBiy5F3jgAuD4Nv32e+EyPB64E6iZadr5Mo0xBx5pKMbSlqC+JNupaPjCWBcW3HMpqipKe/kMRMZQhIn3ssgWiqKsmzhx4sR169bJjkJZLLJzF/bfcw+wb59+L2G34+DsWaifMAEw6S6tAgJrxBqsca2BZkv1So3KH4Wfzf4ZRhR8wvksh9cBC78KHNui34oJOxaGJ+No9eVwulyneTh7qQJY2ZqDd1uDUEWqWBvgieHey4bjvMmjTvM00elNmjQJ69evXy+EmNRXn5MFTQZgQUN9RcTjqP/DH9H+4INQ0oacOgoLse/CC9A+YIDEdP2rWWnGIrEIze7U8Wo22HDjiBvx5QlfRtAV/GifsOsE8MbPINY/CgWp98mdkUIs9l0Jl4kn/taFXfhPUx5OpA0v2aBhfq0NP7/pHOQGzbtJIBmDBY1JsaChvhbeshX7v3EPlIOHetw/OnoU6s4+G3Gf7xRPZjcNGlaL1VjrWgthS723FbgL8K0p38Klgy6FTemlp0pTgfWPAm/8TJ/0CwAxzY6XIpPQUDXftHNlOhI2vHEiF9u6en5/lLvj+Mncgbh45lmSkpHZsKAxKRY01B9ELIaG++9H6/0PwBaL6fcTTgcOT5mC+kmToDmdp/kM2atFacFibTGOeY71uD8yfyS+MeUbmF4+/cMPCQHsfg14/WfA8a09PrQhVI4VuZfDUTykP2NLE9EUrGwNYHWbX1+KDQAuRcVVQ5z4wfWzkRtgrwz1HRY0JsWChvpTvKEB+370Y2jLl/e4H/X5cHDmDBwbPRrChMttBQR2ajux1LEUUWfPIyKml0/HPZPuwajC7nkgh9YAr/8UOLCsx+uOx31YJM5FV+U5cDgcMJuEADa0+/FuSwBhref3wFl5cfz0irGYOJI7/lLfY0FjUixoyAhtb76Jw7/8JWyH63vcDwcCqJ8yBUfHjNZXSplJDDEs15Zjq3trj0nDAHBOwRh8oaUF4/f13JgvojmwJDIae8vnw+3PNTKuIWKagvc6fFjVGkCH2rOQKXPHcdeMMnzmU1O4rwz1GxY0JsWChowiVBXHn3wSjX/8E+ytPZd0R30+1E+ehKNjx0J1uyUl7D+d6MRSdSn2evcCH1hhPTkcwX+1tWNaKIp3Q0OwufBiuAuq5ATtR2FVwfp2P1a35XyoRyZoT+CmsQHcPX8ad/ulftcfBY35/jlGRKek2O0ovekmFF91FeofeABtjz4Ge2cnAMAdCmHQ0ndQvXwFGkeORMP4sxAqNs+ut4Wqgu+FffC2duGRXAWL/amJr2u9Hqz1epAb82GsMhEjNfP8vgHgSNSJdW1+bOvyISF6VnN+WwLzh3rxzctnorgwX1JCok+OPTQZgD00JIsWCqH+kUfQ9vAjsLe1fejjbRXlOD5qNJqGDUXCk30rexShoiK6B8PC6zEwvAkOpDbb2+t04O+5Qbzs90PYev6Qtws7hmnDMEIdgQpRAVsW7kEaUm3Y3unF5k4fGqIf3isnaE/giuE+3H3JJJQWFUhISFbGISeTYkFDsmmxGI4tWICmRx6Fo77+wx+32dDoPXfpAAAgAElEQVQ8aBAaRwxHS01NRg9JKUJDSewABkc2YlB4I3xa54de0x63Y9HRQizuGIq2gB9HKo6gvbodwvXh90Of5sMwbRiGakNRKkqhfHC8KoNEVAV7wx5s7fRiX8ij7+ybrswdx5Wj8vDFeRORn/sR9+Yh6iMsaEyKBQ1lCiEE2lesxOEHHoCyalWPzfnep9lsaKusRPOggWiprUU4Px+QvO2/W+1CZXQXqqPbURXdCY8WOunrtrZ5saixHBvig6A4vT0+ptpVNBU1oamyCYmCkx+b4BEe1Gq1qNVqUaVVwQO5vVZCAE1xB/aFPNgd8uBQxAVxkiLGDoGzClTcPLUS82eOhcukuxtT9mBBY1IsaCgTJRobcXjBk2h/6SU4Dxw45etiPi/aKwagbcAAdJSXIVRY2K89OIpQkZtoQkn8IMpidSiN1SE/cfyUr2+MOPBmYwFWdFXhuL281zOXBAS6Al1oLGpEx4AOCO+p3yMLtAKUi3KUa+UoFaXIE3n9OjwV0RQ0xpyoj7hwOOLCoYjrQ5N701V64jh/cAA3nz0Cw2vNu0s0ZR8WNCbFgoYyXXjPHhx+4gmEl74D56FDvb4+Egyiq7gI4bx8RAMBRIJBRIMBxL1eqC4XVJfr5L06QsCOBFxaGG4tjBy1FTlqK/xqK4LqCRTEjyAv0Qg71NN+/caIA6uac7G8YwDqMAA2+8db/yAUgbbcNjQVNSFUFjptcQMk597ki3wUikLkilzkiBwERAA5yIFbuOGGG3bYTzpsJQQQEwoimg1h1Ya2hB1tCTvaEw40x+04HnOiPdH776PCE8f0Kh+unVKLaaMHc+k1ZSSuciIiKbxDhmDoj38MAIg2NODISy+h/c03YduxE/Zw+EOv97S3w9PefsrPJxQFqssFTRHwKR9+/lSaATSjqNfXqVAwBAqGoBFA48kzAOiwKdhTATw+T0HYc+qeGy8AN4DmXnpfVEVFk9KEJjT1mhEAaqMC+fXzsSo+EzFNOelwUW+8NhVDcoFZA3Nx2cSBGDWoEjaTHkRKdDosaIjoI3FXVKD2jjuAO+6A0DR0bNuG428vRWjdWmj79sN5/DhsJ5l7k04RAo5ocvfeBOT1IAQATNgNrBms4PUJxhcBdW4FZ+W9iqXHZp/R620QKHarqM11YHxlALOGlWHqiGp4snAFGlFfY0FDRB+bYrMhOGYMgmPG6Pe0WAytW7eibdNmhOrqEG9ogHb8OGzNzVBCIdgjEdjjcYmpPyxw5p1EfW5SSMPj3dcuRYPHLuBzAPkeBSV+B8qDblQX+jGmqgDjBpYhjyddE50UCxoi6lM2lwsFEyagYMKEU75GjUYRa2vDp/+6HKETR1CitGK0OACf2wnN5ux14m5fyN+9AlO3JE/Tzmn24qr6Of3+NQEgIeLIVY7iUizBkHgcrc4arPjO2Qh6XfB53Ib83onMiAUNERnO7nbDW1KCSLAAu0JO7EI1agpzUZhr3FuS2vAegGRBowgHKouGGfa1S6M+jDnxKgDA4XCiqID7wRB9Upw5RkTSOOyp3gjNQgsubUibY6RwFRJRX2BBQ0TS2NNW46hWKmhEatm54Iokoj7Bv0lEJI3XmXoLip1+axlTcYiYfq3ZuUKJqC+woCEiaXLcqTkzEQsVNC4R1a81h+80rySiM8WChoik6VnQWGd1j1NE9GvV6ZeYhMg8WNAQkTT+tIImevq9+EzFqaV6aODKkReEyERY0BCRNDmetILGQj006UNOws2N8oj6AgsaIpIm1+vUr8Oadd6OPFqXfq148yQmITIP67yDEFHGKcpx69chzTr7fHq1Tv1aCZRJTEJkHixoiEia4rSCJiwsVNCoHfq1PciChqgvsKAhImmKehQ0ztO80ly8WqqgceYNkJiEyDxY0BCRNMWBVEETVVwSkxhICPjShpzcRdUSwxCZBwsaIpKmMMcFW/fippjNg4QFlm67RRgOEQcAxBUXfLnFkhMRmQMLGiKSxmm3oTzXq7dPRMx/oFMgcUK/7nQWwWbn4ZREfYEFDRFJVZmfKmgawxYoaNRm/TriKZGYhMhcWNAQkVTVBamzjJqj5t9cL5hIFTTxHE4IJuorLGiISKqq9IImZv63pPQeGuTVyAtCZDLmf/cgooxWU5gqaFoS5l+6nZdo1K/tRYMlJiEyFxY0RCTV0JLUWUZt8J3mlSYgBAoSR/Smu3qCxDBE5sKChoikGlTsh7176kzI5kdMM+88Gq/WCY8WApBcsh2sGi05EZF5sKAhIqk8Tjtqi/x6+0jIvCud8hNH9es2VwVcbo/ENETmwoKGiKQbXpYadqrvNG9BUxBPFTThYK28IEQmxIKGiKQbURbUrxsi5j2ksih+WL/WikZKTEJkPixoiEi6s6ry9OvjCfNODC6JHdKvHbXTJCYhMh8WNEQk3fjKVEHTpuQgbsIzndxaCHlqcsm2CjuCw2ZLTkRkLixoiEi6XJ8Tg4qTE4OFYsPhLvOtdCqOHdSvW9wDEMjnoZREfYkFDRFlhPFpw0772yUG6SelaQVNV/4oiUmIzIkFDRFlhMk1Bfr1wahbYpL+URHbk2pUTpUXhMikWNAQUUaYNaRQvz4mcqGaaPW2Q4uiJK2HxjfmYolpiMyJBQ0RZYTqAh8G5CU3mlMVBw52meftqTy2H3aoAIBmZzkKq0dITkRkPuZ5xyCirKYoCmYNKdLbu9rMMzG4Irpbv24vnACbjW+9RH2Nf6uIKGOkFzT7I16JSfpWVXSnfq0MmiMrBpGpsaAhooxxztBi/aDKZiUXHYnsf4vKTTSiIHEMABCHE/mTrpSciMicsv/dgohMI9/vwtSBqcnBm5uzf9ipNrxFvz4eGI1gYanENETmxYKGiDLK3NGpH/g7OrN/+XZtJFXQRGovlJiEyNxY0BBRRrlodJl+fUzkIqRm79uUX21FaTy5XFuDDcEpN0hORGRe2ftOQUSmVJHnxfiqXADJYxA2nMjet6mhofX69THfcBRXD5OYhsjcsvedgohM65pJVfr15s4sPX1bCAwLr9WboaFXSAxDZH4saIgo48wfVw5n93KnZgRwLJJ9b1Ul8YPISyRP144pbhTMulVyIiJzy753CSIyvTyfCxeNSs2lWd3kkJjm4xkeWqNfN+RPQ35JhcQ0RObHgoaIMtK1kyv16+3RPES17FnC7Va7MDS0LnVj/M3ywhBZBAsaIspI5w4tRm1hcv5MQnFifbNTcqIzNzK0Eg4kAABNzkoMmH615ERE5seChogyks2m4PbZA/X2mrYciCw4gdsmEhjdtVxvNw//NJwul8RERNbAgoaIMtbVEysRcNsBAJ2KF1vbM7+XZmh4PfxaOwCgyxZA2QV3Sk5EZA0saIgoY/ndDtwyo1Zvv30iB1oG99LYRAITO17X20eqLkcwv+g0TxBRX2FBQ0QZ7QtnD4LPlXyraoMPm9syd/hmeGg1AmoLACCs+JA/73uSExFZBwsaIspo+X4XvnD2YL39dnMO1AzspXFoMUzseENvH6y5FoXl1RITEVkLCxoiyni3nz0Qwffn0sCLZU0eyYk+bELnGz3mzpRc+gPJiYishQUNEWW8oMeJr39quN5e0Z6HtrhdYqKecuPHMa7zbb19eNhtyC8ul5iIyHpY0BBRVvjsjBoML/UDAFTFjpeP+jJjGbcQmN32HOxQAQDHXLWovvy7kkMRWQ8LGiLKCg67Db+6epzerosHsandLTFR0qjQcgyI7QEAaFDQce7P4PX5Jacish4WNESUNSbVFODTU1Incf+nKQ+tEoee8uLHML3tJb29t3guBs/kqdpEMrCgIaKs8qPLRqEqLzkpOKE48O+GIOKa8TmcWgQXtjymH3FwwlGO4hv+AEXJnjOniMyEBQ0RZRW/24E/3TwJ9u66oUn1YeHRoLHzaYSG81ueQEHiGAAgATvaLvgt8orKenmQiPoLCxoiyjrjq/Lwk/mj9PaOSABvncgx5osLgZntL6Imuk2/tWv43Rg04zJjvj4RnRQLGiLKSp+dUYvrJw3Q2yvac7GsuZ8n4wqBKR2vYkzXMv3WrqK5GHbdT/r36xJRr1jQEFFWUhQF9141DucMKdDvvd2ahzdPBPpl+EkRGma2v4AJnUv0ewdyJqLyc/+Aw+Ho+y9IRB8JCxoiylouhw333zoVU6qD+r0VbUE8fywPMa3vJue6tDAubHm0R8/MYd8Y5N/+FHw5gT77OkT08bGgIaKs5nHa8ch/zcDZg/P1e9tDfvzjUBGORJ2f+POXRvfj6sb/xcDIVv3egZxJCNz+LE/SJsogLGiIKOv5XA48dNt0XDchddxAi+rCQ/XFWNSYi87ER3+r86ltOLdlAa448RcEu0/QBoDdRXNRfNeLyC0s7ZPsRNQ3OPBLRKbgsNtw3w0TMWXgAfz4hS2IqgCgYENHDjZ2+DAmJ4yxgRCqPDHYTjEapQgV5bF9GB5ag8HhjbAhtcFNVPFg7+ivY9iV3+acGaIMxL+VRGQq10+twdRBRfjOk2uw+lAXAECDDZs6/djU6YfHpqLUFcdV8VSvTbmrE+c3/RVF8Xq4RORDn/OQ/ywol/wGo0bPMOz3QUQfDQsaIjKd2iI/nvzSuXhtSwN+u2grdjfH9Y9FNDsOROwIpU0aLrSHUBE79KHPc9Q9GJ0T70LtBZ9nrwxRhuPfUCIyJUVRMHfsAMwdOwCr9zbi4be3Y3ldO1pjyUJGPcUUwg57Pk4UTgHG34TKqfNRxkKGKCvwbyoRmd7UwcWYOrgYQgjsPdaOdXsaUPfWZGxwnEBC1VA+fCQOz7gY7qrxyB84HrXOT746ioiMxYKGiCxDURQMKcvFkLJcYPa9AO6VHYmI+giXbRMREVHWY0FDREREWY8FDREREWU9FjRERESU9VjQEBERUdZjQUNERERZjwUNERERZT0WNERERJT1WNAQERFR1mNBQ0RERFmPBQ0RERFlPRY0RERElPVY0BAREVHWY0FDREREWY8FDREREWU9FjRERESU9VjQEBERUdZjQUNERERZjwUNERERZT0WNERERJT1WNAQERFR1mNBQ0RERFmPBQ0RERFlPRY0RERElPVY0BAREVHWY0FDREREWY8FDREREWU9FjRERESU9VjQEBERUdZjQUNERERZjwUNERERZT0WNERERJT1WNAQERFR1mNBQ0RERFmPBQ0RERFlPRY0RERElPVY0BAREVHWY0FDREREWY8FDREREWU9FjRERESU9VjQEBERUdZjQUNERERZjwUNERERZT0WNERERJT1WNAQERFR1mNBQ0RERFmPBQ0RERFlPRY0RERElPVY0BAREVHWs1RBoyjKUEVRvqsoyhJFUQ4pihJTFOWYoigvKIpyXi/P3qooympFUToVRWlTFOUtRVEuMyo7ERERnZqlChoAvwDwfwCUAngFwO8ALANwKYAliqJ89WQPKYryWwAPAygH8ACAxwGMBbBQUZS7+z82ERERnY5DdgCDvQrgN0KIDek3FUU5F8BiAPcpivKUEOJI2sdmAvgmgL0ApgghWrrv3wdgHYDfKorykhCizqDfAxEREX2ApXpohBAPf7CY6b7/NoC3ALgAzPzAh+/s/vWX7xcz3c/UAfgzADeAz/dHXiIiIjozlipoehHv/jXxgfvnd//66kmeWfSB1xAREZEEihBCdgbpFEWpAbATgAqgMm1YyQ+gE0CnECJwkueKADQCOC6EKD2Dr7PuFB86y+v12keOHPlxfwtERERZY/v27QiHw81CiMK++pxWm0PzIYqiuAH8E8mho++kDysByO3+te0Uj79/P+8TxrCFw2F1/fr1Gz/h5yHjjej+dYfUFPRx8c8vu/HP7/9v786j5S7rO46/PyQFgQhhkaUtWwUBqSwCEQhLQhRwoaCFRpaAoSyRJbKdUmUxIFqOWkCo7IQgSSx7ELAKLV4sCYjsAkIQvUdkFZIGCFkg+faP5xkyDjNz5947d2Z+N5/XOfc88Fue33fmx/D7zrNNcW0DDGtmhYVLaCR1Axv14pRpEXFojbqGANcBI4Hrge/3MayGmrkiYvsacTxcb791Lt+7YvP9Kzbfv+Kq02PRZ4VLaEizjRb24viXqm3MycxU4EDgBuDQ+GD/W6kFZnWq66kFx8zMzFqgcAlNRIzpbx2ShgLTScnMdOCwiFhS5VrzJb0I/I2k9cunc2eb5XJ2f2MyMzOzvlvuZjlJWhG4iZTM/AgYVy2ZKXNPLvepsu+zFceYmZlZGyxXCU0eAHwrsB9wNTA+Ipb2cNpluTxd0hpldW0MHAcsAq5perBmZmbWsMJ1OfXTZcDngNeBF4GzJFUe0xURXaV/iYhZks4HTgaekHQTaQG+scCawAleJdjMzKy9lqt1aCR1AXv0cNjZETGpyrmHA8cDHweWAo8A34uIO5ocppmZmfXScpXQmJmZ2eC0XI2hMTMzs8HJCY2ZmZkVnhMaMzMzKzwnNGZmZlZ4TmjMzMys8JzQmJmZWeE5oSkASVdLivy3abvjsdokbSbpNEn3SHpB0mJJr0q6TdLodsdniaS/lTRZ0kuSFknqlnRh+Wrg1nkkrSXpSEm3SvqdpAWS5km6T9I/S/IzrWAkjSt7vh3Zr7q8Dk1nk7Qv8BPgbWAYsFlE/K69UVktkv6TtIr008B9wBxgc+AfgCHA1yLiovZFaJI+CswC1gFuA54BRgCjgWeBkRHxRvsitFokTQAuBV4GfgH8EVgX+BKwOnAzcGD4wVYIkjYAfkP6f+Mw4KiIuKrP9fm+dy5JHyHd7C5gPdIqx05oOpikrwCPR8SjFdv3AO4GAti4yi+3W4tI+jmwFzAxIi4u234+cBJweURMaFd8VpukPYFVgTvLf4dP0nrAg8AGwAERcXObQrQGKf3u0N3AJsAtwKn0M6Fx81xnuyKXx7U1CmtYREypTGby9ntJiemKwC6tjssSSX9HSma6gR9W7P4mMB8YJ2nVFodmDYiIeyLi9sofFY6IV1j2Q8KjWh6Y9cVEYE9gPOlz129OaDpU/qa/PzDBzd+Dxru5fK+tUSzf9szlXVUeim8BM4FVgJ1aHZj1mz9fBSFpS+A84AcR8ctm1euEpgNJ2gj4ATA1Ima0Ox7rv3xPxwDvAE37AFuvbZ7L2TX2P5fLj7UgFmsSSUOBw/K//qydsVh9+V5dRxr/9I1m1j20mZVZ/+VR+teSBgFPbHM41gSSVgKmASsB/xIRc9sc0vJs9VzOq7G/tH14C2Kx5jkP+HvgpxHx83YHY3WdBWwH7BoRC5pZsVtoBkCeAhq9+JtadvpJpMG/R/nB1x79vH+VdQ0hfRsZCVwPfL9Vr8P6RLn0bImCkDQROIU0W21cm8OxOiSNILXK/HtE3N/s+t1CMzCeBxb24viXIK1hAnwbuCYifjoQgVlD+nT/KuVkZipwIHADcKink7ZdqQVm9Rr7V6s4zjqYpONI3fNPA2MiYk6bQ7IayrqaZgNnDsQ1nNAMgIgY08dTtyJ1S4yXNL7GMc+l2W580eNrBkY/7t/78od3OimZmQ4cFhFL+luv9duzuaw1RmazXNYaY2MdQtKJwAXAk6Rk5rU2h2T1DWPZ525hfo5VulLSlaTBwif29gJOaDpLN3B1jX2fJ61FcyPwZj7WOpCkFUktMvsBPwLGV86osbb5RS73krRCxVomHyZ1DS4AHmhHcNYYSaeRxs08BnwmIl5vc0jWs0XUfr59kjSu5j7Sl44+dUd5Yb2CkNSFF9breHkA8C3A50gf3qOdzHQWL6xXbJLOBM4BHgb2cjdT8UmaRFoHql8L67mFxqy5LiMlM68DLwJnVWla7YqIrhbHZcscS/rpg4skjQF+C3yK9NMHs4HT2xib1SHpcFIyswT4X2Bilc9Xd0RMaXFo1gGc0Jg11ya5XJs0PbGWroEPxaqJiOcl7UB6MO5DSkBfBi4CzvY3/o5W+nwNAWqNsbgXmNKSaKyjuMvJzMzMCs/r0JiZmVnhOaExMzOzwnNCY2ZmZoXnhMbMzMwKzwmNmZmZFZ4TGjMzMys8JzRmZmZWeE5ozMzMrPCc0JiZmVnhOaExMzOzwnNCY2ZmZoXnhMbMlmuSNpYUkqa04FpH5GuNqNgekroG+vrtIuliSXMlrd3uWGzwckJj1kHyg63uL8ZK6s7HbdyaqJpP0pX5NbwjaXi742kFScOAc4HbI+LBdsfTYt8GVgImtTkOG8Sc0JhZS0n6MPBlIICVgUPbG1HLTATWB85rdyCtFhGvAFOAYyRt2OZwbJByQmNmrXYwMAy4EFgMHNXecAaepCHABOC5iJjV7nja5FpgKHB0uwOxwckJjdkgImmMpJ9JmiNpoaTZks6TtHqVY7slddeoZ1LuEhpVsT0kdUlaT9JVkl6UtETSV3oR5lHAUuAC4A5ga0mfqhHHlFL3mqRjJP0mv65XJV1R7XXl8/aWNFPS/PxezJC0RXl9jQQqaRVJX5f0WK7rbUn3SzqoF68X4DPABsD1PVxv7fy6Xpa0SNJTksbXOHYFSRMk/TrHNT//81clrVBxbN1xQvmeRsW2UfmcSZJGSLozv5fvv3+Stpb04/zf0iJJf5b0iKQLJf1VeX0R8SugGzhCkuq9D2Z9MbTdAZhZc0g6BrgUmA/cCLwGjAJOA/aVNDIi/q8Jl1oTeAB4G7iFlJy82mCM2wHbA3dHxAv5Afsl0rf2X9U59bvA3sDtwF3AaFJitCmwZ8U1xgLTgUXADcDLwC7A/cDjjcSZ6xkO3ANsBzwCTCZ9CdwbmC5pq4g4o8HqPp3L++ocMxyYSWq1ugn4EHAAMFnS0oi4tuL460itXS8AV5G68L4IXALsChzSYGw92Rn4eo59MrA2sFjS1qR7FsBPgD8Aq5HuybHAGcC7FXXNzHFtBTzZpPjMACc0Zh1J0qQ6uz8wiFbSRsBFpCRjREQ8U7bvEuCrpKSgGc39nyA9TI+IiPd6ee4xubwml/9FSobGSjopIt6scd5OwCci4o8AkoaSko3RkkaUBtnm8TmXAe8BO0fE+wmMpPNIyV2jLiQlM6dFxHfL6vkQMAP4hqSbIuKxBuraNZcP1TlmG+Bq4JiIWJKvdQHwRI77/YQmtxAdDDwK7B4Rb+ftZwD3AgdLujMipjf0SuvbC5gQEZeXb5R0Cinp2j8ibqvYtwbwTpW6fk1KaHbHCY01mbuczDrTN+v8VetmORRYEfiP8mQmOx14CxgnaaUmxLYYOLW3yYykVYGDgHnArQC5jmnAqqQHdC3nlJKZsvNKSVH5FOj9SAnftPJkJjsXaKiFStJapPf0ofJkJl97ISnBUA8xl9sQeDci3qhzzDvAyaVkJl/raVKrxpY5WSs5Ipf/Wkpm8vHzWZa0HdlgbD15rDKZqbCgckNEzI2IpVWOfSWXHhhsTecWGrMOFBE1xxjkcS8bVWz+ZC7vqVLXXEmPkr4Vb0Evul1q6I6I1/pw3pdJXRKX56Sg5BrgZFLr0WU1zq3WsvFCLtco27ZdLj/QtRMRb0t6jNQN15MdgSFA1GgtK40P2bKBugDWAub2cMxzNVqoSq9zOCkxhXS/lwJdVY6/F1jCsveiv2pNMb8e+BowQ9JNwH8DMyPi+Tp1zcml16OxpnNCYzY4lFptXq6xv7S9GWu+vNLzIVWVurumlG+MiCclPQxsL2mHiKiWvFRrWSm1EA0p21Z6H2qN6WlorA8pAYGU2OxY57hhDda3gNQ9U0+t1qNar3NORCyuPDgi3pP0OrBOg7H1pOr9jogHJe1GagE8ABgHIOlZ4OyI+HGV01bO5Qdadcz6y11OZoPDvFyuV2P/+hXHQfqGX+tLTb3Ep+7Cf9XkAaSlrqH780yZ9/9IA4Wh/2N8Si0c69bYX2t7pdL7dEFEqM7f6Abrew1YrXLmTz/MA9asVl8eX7Q2y94LSPcamny/I+L+iPgCqZVsJPAt0ns8XdKnq5xSShT70sJnVpcTGrPB4dFcjqrckWfrbAssBH5btmsusG6Nh+wOTY6vlKh0kQa+VvtbAByktKJuX5Xeh10rd+R6t22wngdJScBu/Yil3BO53LxJ9T1K+v/37lX27U5qzXmkbFupu2uDyoMlrQZ8rD/BRMSiiJgVEWeRFhCENJ6p0ha5bGQgtVmvOKExGxymkqbIniBp04p93yKNXZkaEYvKtj9I+sb+F+uc5DVlRjYrMEkrk2a2LAEOiYgjq/0BN5O6cHq7xku520itF4dI2qZi3xk02OWWxwhNA3aQdGZu9fgLkj4qaZMG4+rK5U4NHt+Tybn8N0mrlMW0CstWIr66tD0i3gKeAUZK+njZ8UOA81nWFdQwSbvVWAeo1ApWbZbTTqT/Dn7Z2+uZ9cRjaMwGgYjolnQi8EPgEUk3AH8G9iCtI/IMH5yyfDEpmblU0hjS4NNtSGu23AF8oUnhjSUlErdHxEt1jruKNLPoaODKvlwoIt6UdCwpwZuV34fSOjTbkAbM7sGyLph6jgc2A84hzRC7jzQG569Jg4F3JCVff2igrhmkaeB7k15nv0TEdEn7Af8EPCVpBqlraH9gE+CGiJhWcdr3SEnOTEk3klrsRpMGOD9Oen964xRgL6Uf1fw9acmArYDPklqErig/OCc/I4D/iYh5mDWZW2jMBomIuIT0wHwA+EfSzKF1SA+ynSNiTsXxT5MWfJsJ7EtKJBaTEqCHmxha6acN6j7II+JeYDapVaTPM3Ty2iufJz2kx5LW4JlHel2lKc611rspr+dNUvJzAvA6y97T0aTZRicBdzcY059IiwLum9doaYaDgOOAN0jr+0wgJRLHU6WVKyImk6ZyvwQcTkqGZpFa4/qy4OIlpJlOG5MGBJ9A6rq6BNiuymynsaSB0Zf24VpmPVJEr8f3mZkVTu5e+T2wUkTUGjw9kNffhZQ8nhwRF7T6+u0m6SFSl+JW5WvtmDWLW2jMbFCRNLx8XEneJtIYmg1JP9fQcvlHKZHTjUkAAADTSURBVG8ETquMb7CTtD9pJtupTmZsoLiFxswGFUn7kLpC7iL9GOIw0mDUbUnjhHbo48KAzYhtQ9IqvzdGxFPtiKEd8k81rBsRF7Y7Fhu8nNCY2aCSZx6dSxob8hHS5Ic/kQY6fyciGl1cz8wKxAmNmZmZFZ7H0JiZmVnhOaExMzOzwnNCY2ZmZoXnhMbMzMwKzwmNmZmZFZ4TGjMzMys8JzRmZmZWeE5ozMzMrPCc0JiZmVnhOaExMzOzwnNCY2ZmZoXnhMbMzMwKzwmNmZmZFd7/A4MM97jqpgp2AAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 288x576 with 1 Axes>"
      ]
     },
     "metadata": {
      "image/png": {
       "height": 479,
       "width": 282
      },
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "plt.figure(figsize=(4, 8))\n",
    "plt.plot(df_HET.h_ha1, df_HET.h_dec, label='1')\n",
    "plt.plot(df_HET.h_ha2, df_HET.h_dec, label='2')\n",
    "plt.plot(df_HET.h_ha3, df_HET.h_dec, label='3')\n",
    "plt.plot(df_HET.h_ha4, df_HET.h_dec, label='4')\n",
    "plt.fill_betweenx(df_HET.h_dec, df_HET.h_ha1, df_HET.h_ha2, color='#000000', alpha=0.4)\n",
    "plt.fill_betweenx(df_HET.h_dec, df_HET.h_ha3, df_HET.h_ha4, color='#000000', alpha=0.4)\n",
    "plt.xlim(-4, 4); plt.ylim(-20, 90); plt.legend();\n",
    "plt.xlabel('Hour Angle (hours)'); plt.ylabel('Declination (degrees)');"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Not bad!  We have replicated the constraints.  Let's now make a custom `astroplan` constraint, inheriting from the generic base class `Constraint`."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 15,
   "metadata": {},
   "outputs": [],
   "source": [
    "from astroplan import Constraint"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 16,
   "metadata": {},
   "outputs": [],
   "source": [
    "class HETConstraint(Constraint):\n",
    "    \"\"\"\n",
    "    Constraint based on HET tracking for fixed Azimuth\n",
    "    \"\"\"\n",
    "    def __init__(self):\n",
    "        \"\"\"\n",
    "        min : `~astropy.units.Quantity` or `None` (optional)\n",
    "            Minimum acceptable separation between Vega and target. `None`\n",
    "            indicates no limit.\n",
    "        max : `~astropy.units.Quantity` or `None` (optional)\n",
    "            Minimum acceptable separation between Vega and target. `None`\n",
    "            indicates no limit.\n",
    "        \"\"\"\n",
    "        \n",
    "        # put in HET stuff here\n",
    "        self.h_dec = df_HET.h_dec.values*u.deg\n",
    "        self.ha_min = df_HET.ha_min.values*u.hourangle\n",
    "        self.ha_max = df_HET.ha_max.values*u.hourangle\n",
    "        self.h_ha3 = df_HET.h_ha3.values*u.hourangle\n",
    "        self.h_ha4 = df_HET.h_ha4.values*u.hourangle\n",
    "\n",
    "    def compute_constraint(self, times, observer, targets):\n",
    "\n",
    "         if targets.isscalar:\n",
    "    \n",
    "            ha = observer.target_hour_angle(times, targets, grid_times_targets=False).wrap_at(12*u.hourangle)\n",
    "\n",
    "            idx = np.abs(targets.dec - self.h_dec).argmin()\n",
    "            e_lo, e_hi, w_lo, w_hi = (self.h_ha4[idx],self.h_ha3[idx], self.ha_min[idx], self.ha_max[idx])\n",
    "\n",
    "            return ((ha > e_lo) & (ha < e_hi) ) | ((ha > w_lo) & (ha < w_hi)) \n",
    "         else:\n",
    "            hour_angles = observer.target_hour_angle(times, targets, grid_times_targets=True).wrap_at(12*u.hourangle)\n",
    "\n",
    "            indices = [np.abs(target.dec - self.h_dec).argmin() for target in targets]\n",
    "            boundaries = [(self.h_ha4[idx],self.h_ha3[idx], self.ha_min[idx], self.ha_max[idx]) for idx in indices] \n",
    "\n",
    "            mask_out = np.zeros_like(hour_angles.value, dtype=bool)\n",
    "            for i, ha in enumerate(hour_angles):\n",
    "                e_lo, e_hi, w_lo, w_hi = boundaries[i]\n",
    "                mask_out[i:] = ((ha > e_lo) & (ha < e_hi) ) | ((ha > w_lo) & (ha < w_hi)) \n",
    "\n",
    "            return mask_out\n",
    "       "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 17,
   "metadata": {},
   "outputs": [],
   "source": [
    "con3 = HETConstraint()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### HETDEX \n",
    "\n",
    "During its core Dark Energy Experiment, HETDEX essentially takes up 100% of the dark time, so most observations will also require gray or bright time.  If you have priority 0 time, you can override this constraint, so your science may choose to toggle this requirement on or off."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 18,
   "metadata": {},
   "outputs": [],
   "source": [
    "con4 = astroplan.MoonIlluminationConstraint(min=0.4, max=1.0)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Putting it all together: many constraints.\n",
    "\n",
    "We will finally combine all the constraints.  In practice it takes a couple minutes to check all of the constraints for all of the sources."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 19,
   "metadata": {},
   "outputs": [],
   "source": [
    "all_constraints = [con1, con2, con3, con4]"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 20,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "CPU times: user 35.9 s, sys: 5.64 ms, total: 35.9 s\n",
      "Wall time: 35.9 s\n"
     ]
    }
   ],
   "source": [
    "%%time\n",
    "table = observability_table(all_constraints, het, targets, time_range=time_range, time_grid_resolution=0.25*u.hour)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 21,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>target name</th>\n",
       "      <th>ever observable</th>\n",
       "      <th>always observable</th>\n",
       "      <th>fraction of time observable</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>7</th>\n",
       "      <td>Merak</td>\n",
       "      <td>True</td>\n",
       "      <td>False</td>\n",
       "      <td>0.062652</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>8</th>\n",
       "      <td>Mizar</td>\n",
       "      <td>True</td>\n",
       "      <td>False</td>\n",
       "      <td>0.041129</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>1</th>\n",
       "      <td>Castor</td>\n",
       "      <td>True</td>\n",
       "      <td>False</td>\n",
       "      <td>0.039038</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2</th>\n",
       "      <td>Pollux</td>\n",
       "      <td>True</td>\n",
       "      <td>False</td>\n",
       "      <td>0.037818</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>5</th>\n",
       "      <td>Betelgeuse</td>\n",
       "      <td>True</td>\n",
       "      <td>False</td>\n",
       "      <td>0.031893</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>3</th>\n",
       "      <td>Aldebaran</td>\n",
       "      <td>True</td>\n",
       "      <td>False</td>\n",
       "      <td>0.025096</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>6</th>\n",
       "      <td>Alpheratz</td>\n",
       "      <td>True</td>\n",
       "      <td>False</td>\n",
       "      <td>0.008975</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>0</th>\n",
       "      <td>Sirius</td>\n",
       "      <td>True</td>\n",
       "      <td>False</td>\n",
       "      <td>0.000436</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>4</th>\n",
       "      <td>Polaris</td>\n",
       "      <td>False</td>\n",
       "      <td>False</td>\n",
       "      <td>0.000000</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "  target name  ever observable  always observable  fraction of time observable\n",
       "7       Merak             True              False                     0.062652\n",
       "8       Mizar             True              False                     0.041129\n",
       "1      Castor             True              False                     0.039038\n",
       "2      Pollux             True              False                     0.037818\n",
       "5  Betelgeuse             True              False                     0.031893\n",
       "3   Aldebaran             True              False                     0.025096\n",
       "6   Alpheratz             True              False                     0.008975\n",
       "0      Sirius             True              False                     0.000436\n",
       "4     Polaris            False              False                     0.000000"
      ]
     },
     "execution_count": 21,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "obsservability_df = table.to_pandas()\n",
    "obsservability_df.sort_values('fraction of time observable', ascending=False)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Hooray!  We have compiled the constraints into a rank-ordered list of HET observability for the trimester.  "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Bonus: Visualize the constraints\n",
    "\n",
    "We can spot-check the constraints by visualizing them for a particular object on a particular night.  \n",
    "See the `astroplan` [documentation](https://astroplan.readthedocs.io/en/latest/index.html) for more examples like this one."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 22,
   "metadata": {},
   "outputs": [],
   "source": [
    "from astroplan.utils import time_grid_from_range"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 23,
   "metadata": {},
   "outputs": [],
   "source": [
    "target = FixedTarget(SkyCoord.from_name(\"Merak\"))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 24,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAC3UAAAEuCAYAAACTG9p4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAWJQAAFiUBSVIk8AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nOzcebhkVX0u4O/XNFMSBYkGUKM4cBUVh241DhBARdSgktyg15goqMQhiTgkKgS1cR4ioteb64CmxQHnaFCjItoaJVe0nXBGoQWRQcBGZhp63T/2PloUdZpzTg+7i37f56lnW3utvde3q6rxn++saq0FAAAAAAAAAAAAAIBhLBo6AAAAAAAAAAAAAADAlkypGwAAAAAAAAAAAABgQErdAAAAAAAAAAAAAAADUuoGAAAAAAAAAAAAABiQUjcAAAAAAAAAAAAAwICUugEAAAAAAAAAAAAABqTUDQAAAAAAAAAAAAAwIKVuAAAAAAAAAAAAAIABKXUDAAAAAAAAAAAAAAxIqRsAAAAAAAAAAAAAYEBK3QAAAAAAAAAAAAAAA1LqBgAAAAAAAAAAAAAY0OKhAwCsj6o6M8nNk6waOAoAAAAAAAAAAACwZdstyW9aa3eY74VK3cC0u/n222+/0x577LHT6d88Y+gsc7L7kjte7/205E5kH8K05k5uWtmz5vvDBJmvre9+/ffTkjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmjuRfQjTmrv3w9OvyXbb1k4LubZaaxs6D8AmU1UrlyxZsmTlypXZf9HBQ8eZk5PWfvh676cldyL7EKY1d3LTyr72vN0HSjI/i3Y5/XrvpyV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjV3IvsQpjX3jPs9/OwkycrvXlXzvXbRBk8DAAAAAAAAAAAAAMCcKXUDAAAAAAAAAAAAAAxIqRsAAAAAAAAAAAAAYEBK3QAAAAAAAAAAAAAAA1LqBgAAAAAAAAAAAAAYkFI3AAAAAAAAAAAAAMCAlLoBAAAAAAAAAAAAAAak1A0AAAAAAAAAAAAAMCClbgAAAAAAAAAAAACAASl1AwAAAAAAAAAAAAAMSKkbAAAAAAAAAAAAAGBASt0AAAAAAAAAAAAAAANS6gYAAAAAAAAAAAAAGJBSNwAAAAAAAAAAAADAgJS656mqllVVq6p9x863qloxTKrJqmq3PtfyobOMq6rlfbbdhs7Cjducf0sAAAAAAAAAAAAA0269S9190bNV1dqqutM65n1xZO4h67vuxlZVhyixLtxs5ffNSVXdtar+d1V9r6ouqaprquqXVfWpqnpqVW03dMbZVNWKqmpD51iIqlpVVauGzgEAAAAAAAAAAACwuVi8ge5zbX+vpyY5cnywqnZPss/IPDaNc5LskeSSoYNMcESS16TLuMlV1UuSvDTdHzb8vyTvTnJZkp2T7JvkuCTPTHLfIfJthjbn3xIAAAAAAAAAAADAVNtQBevzk5yb5NCqeklr7dqx8aclqSSfTHLQBlqTG9FaW5PkR0PnmKS1dm6638wmV1VHJjk6ydlJDm6tfW3CnAOTPH9TZ9tcbc6/JQAAAAAAAAAAAIBpt2gD3usdSXZJcuDoyaraOsmTk5yS5PuzXVxVu1fV8VV1TlVdU1W/7N/vPsv8Harq1VX146q6qqp+XVWfraqHTZi7b1W1qlpWVfeuqk9V1eqquqKqvlRVD1qvJ5/9mZb36+62rkxj51f057euqpdU1c/65/tRVR02Mu8ZVXVaVV1ZVb+oqqOratHYvXbr77V8tlxV9fT+PldV1flV9faq2mFC3v36sR9U1W/6db9XVS+tqu3G5q5Ktwt2knyxX6tVVZvjZ/O4qvpyVV3Sr3NaVR1RVdtOmLuqf/1eVb2+qs6qqqur6qdV9cKqqvHPJMmyJGuSPGpSoTtJWmufTPKITZmtv+YxVXVyVZ3bz/1l/xt91kz+/nPcp3/fRl4rJqx986o6pv/fa2Z+b1V16/739dWqOq9+92/u/VW1x4Rc6/1bmvnNJ7l9ktuPZV8eAAAAAAAAAAAAgC3UhtqpO0lOSHJMul25Pz5y/jFJdk7yoiR3nnRhVd0vyeeT3CzJfyT5QZK7JnliksdW1UNba98Ymb9jkq8muVuSryc5Nsktkzwuyeeq6pmttbdNWOq+SV6Q5L+THJfkdkn+Z5KTq+rerbUfL+zRN4oPJPmTJJ9OV0D+yyRvr6o1Se6Zrij/ySQnp/uMX5LkiiSvnccar0tyQJITk3wuyX5JDkv3PT1kbO4L030npyT5VJLtkjw4XUF636p6WGvtun7usel2ZN8nybuTrJproKp6VZIjklyY5P1JLkvyyCSvSnJAVe3f7xo9aus+/62T/GeSa/v1X9PnPHpk7qH9/A+01r63riyttas3Zbaq+tskb0tyXrrv5MIkf5Tu+z40yb8mWd1fc0i6cvTos60aW3ubJF9IslOf4TdJzuzH/jTdv8kvJvlo/yy7p/udPaaqHtxa+866Pp8xc/ktrerzPqd/f+zI9d+ex1oAAAAAAAAAAAAANykbrNTdWru0qj6Q5JCqum1r7Rf90GHpyqQfSnLk+HX9bsXHJ7l5kr9urb1vZOzx6crN762qu7XW1vZDr01X6H57kme01lo//7VJvpHkzVX12dbaqrHl/izJoa215SNrPD3JW5McnuRZ6/ERbGi3S3KP1trqJKmqNyT5UZI3piv23rO1dk4/tizJT5P8Y1W9obV27RzXeECSPVtrZ/X3WZyuBLxfVd2/tXbqyNxnJTlz5rOeUVUvT3JUujLwB5OktXZsX7zfJ8ny1tqKuYSpqgemK02fneT+rbXz+vNHJPn3dLvA/1O6EvWoWyf5TpL9W2tX9tccneQnSZ5bVa8aKVvv1R9PnkumTZzt6UmuSXKv1toFY+vfMkn638Oyqto3ye1ba8vWEXvXdH8gsU9r7fKxsS8k2bm1dunYOvdK9wcTr0lXWJ+rG/0t9f8el1XVIf2zrCs7AAAAAAAAAAAAwBZj0Qa+3zuSbJXkKUlSVbdPsn+S97XWrpjlmgel2wH6v0cL3UnSWvtgkq8kuUv6Mm5VbZ3kr9PtLHzEaMm4tXZ6kjen26H4SRPW+upoobv3rnS7J99/zk+5abxoptCdJK21M9J9FjsmeflMobsfW51uh+RbJrnNPNZ42UwJt7/PtUn+rX97vc+jtXbGeKG7N7Pb8gHzWHc2T+mPr5gpTY/ken6Stel2gp/k2TOl6f6aC5J8IskO6X4/M3btj7/I/GyKbEn3Wxzf7TuttQvnmXfG8ycUutNau2C80N2f/05+V8beeh7rzPm3tFBVtXLSK91/PwAAAAAAAAAAAACm1gYtdbfWvpbktCRPqapF6Uqui9KVvWezpD9+YZbxmfP36Y93TfJ7Sb7TWrt4DvNHfWNC5jVJzk9yi3VkHMINsib5ZX9cOWFspuR92/Vc4+z+eL3Po6p+v6qOrKqvV9UlVbW2qlqSmbLxfMrks5n1t9Ba+0m6IvYd+l3AR13SWvvphPtNepaaueVmmO196X7b36+qN1bVQVV1q3nmHHVVku/ONlhVf1ZVJ1bVuVW1pqpa/50+Osm26f5IYK7m/FsCAAAAAAAAAAAA4PoWb4R7viPdbtmPSHJokpWttW+tY/4O/fHcWcZnzs+UZec7f9TqCeeSbnfkrWYLOITW2iUTTl/bH9c1Np/dlSd9HjP3+e3n0e/Y/IV0Oy5/L8kHk/wqv9tR+qXpSsDray7f7e36eaPZ1/W9Jtf/bn+Z7g8D5lN+3yTZWmvHVNWFSZ6V5NlJnpOkVdWXkvxTa21ScXpdLphld/VU1bOTvCnJr5OclOSsJFekK7sflORemd93Oqff0vporS2ddL7frXvJpDEAAAAAAAAAAACAabAxSt3vSfLaJG9Lt3vzy25k/kxBeZdZxncdmzff+UNa2x8nfc6TSuebq8emK3S/u7V2yOhAVe2artS9IYx+tz+bML4hvtuvJHlIkocmeec8rtsU2dJaOz7J8f2O3w9K8udJnpLks1W1R2vtgvncbtLJqlqc5Ogk5yVZ0lo7d2z8gQsKDwAAAAAAAAAAAMCCLNrQN2ytrU7ykXQ7IV+e5IQbuWRmF+99ZxmfOf/N/vjjdDsK37uqbjFh/n5j84f06/74xxPG7rspg6ynO/fHj04Y22eWa67rj/PZpXnW30JV3Tndb+rM/je2UP+Wbofx/1lVd1vXxKoa3al6U2T7rdba6tbap1trhyVZnmSnJHuPTLmuX3shu2DfMt0fFZwyodD9B9n4u15fl81sZ3wAAAAAAAAAAACAIW3wUnfvqHQ7DB/QWrv0RuZ+NV1Re6+q+svRgf79nyb5SbodltNauybJ+5L8QcZ2Aa+qOyV5drrS7nvW/zHW26n98bDRk1W1Z5LDN32cBVvVH/cdPVlVd0y3K/skF/XH281jnXf1x6Oq6lYj62yV5F/S/V7ns7v2DbTWViVZlmSbJJ+qqonl+qp6RJL/3JTZquoR/S7a4/6oP14xcm4hn++MC/p7Le1L3DPrb53kTelK3xvTRUluVVXbb+R1AAAAAAAAAAAAAKbCpALpemutnZXkrDnObVX15CQnJflgVX0iyY+S3CXJQUkuTfKk1trakctelG7X4r+vqvsl+WK6Iurjktwsyd+31s7cUM+zHj6R5PQkT6iq2yb5WroS7mP7sccNmG0+Tkzy0yTP6wvp30r3HAcm+VQmF4u/mGRtkldX1T3S71reWnvFbIu01k6pqtcleUGS71XVR9Lt9v7IJPdIV+x//fo+TGvtVX15+qVJvl5VpyT5RpLLkuyc7g8Jdu/PbcpsH0hyVVV9JV2RvtL9zu+XZGWSz4/MPTnJwUk+VlWfTnJlkp+31m70jxlaa2ur6s3p/h2d1v+b2ybdLvc7pfvu9lvHLdbXyeme6TNV9eUkVyf5TmvtxI24JgAAAAAAAAAAAMBma6OUuuertfa1vpx9VJKHJXl0kguTnJDk5a21H4/Nv7iqHpjkiCR/keR56UqtpyZ5fWvtc5sy/2xaa1dV1UPT7eS8f7oi6/eS/FWSizMlpe7W2uVV9ZAkr0m3W/feSc5I8vIkxyR5/IRrftiX9f8xybOSbNcPzVrq7q97YVV9K8nfJ3lSkq2T/Czdb+MN/U7tG+KZXlZVH+6z7Zfk0D7jRUm+nW4H8vdu4mwvSnJAkiVJHpXkqiQ/T/LCJP+3tbZmZO5xSW6f5H+lK5ovTvKlzH2H+hcn+VWSpyV5epJL0v1hxVFJjl7P57gxr0iyY7p/5w9OslWSd6f74wEAAAAAAAAAAACALc56l7pbazWPuUelK41OGvtxkr+Zx71Wpyu7vnAOc1ek2/V4tvHdJpxbnmT5hPPLkiybcH7i/VtrZ2dC6bl3g2taa/uuI+chSQ6ZZewGuVprq2ZZY133WTHLNWcneeIs0WZ79vdmrBg9xwwfSLdr9Y2a9N2NjC3LhO9qZPyHSf5hLutsimyttbcmeesc731dkiP717zW7sevTVfIP2bC8CEZ+2428G/p8iTP7F8AAAAAAAAAAAAAW7xFQwcAAAAAAAAAAAAAANiSKXUDAAAAAAAAAAAAAAxIqRsAAAAAAAAAAAAAYEBK3QAAAAAAAAAAAAAAA1LqBgAAAAAAAAAAAAAYkFI3AAAAAAAAAAAAAMCAlLoBAAAAAAAAAAAAAAak1A0AAAAAAAAAAAAAMCClbgAAAAAAAAAAAACAASl1AwAAAAAAAAAAAAAMSKkbAAAAAAAAAAAAAGBASt0AAAAAAAAAAAAAAANS6gYAAAAAAAAAAAAAGFC11obOALBgVbVyyZIlS1auXDl0FAAAAAAAAAAAAGALtnTp0mTN97Pyu1fVfK9dvDECAWxMVXWzJDfr3269du3aIeMAAAAAAAAAAAAArJdFQwcAWIDnJzmnf+15/vnnDxwHAAAAAAAAAAAAIDn9tO0XdJ1SNzCN3pDkNv3rtJ133nngOAAAAAAAAAAAAAALt3joAADz1Vq7NMmlSVJVaxYt6v4+Zf9FBw8Za85OWvvh672fltyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tyJ7EOY1tzJDbOvPW/3gZLM36JdTr/e+2nJPq25E9mHMK25E9mHMJ57mv//SPaNb1pzJ7IPYVpzzzi9nbHga+3UDQAAAAAAAAAAAAAwIKVuAAAAAAAAAAAAAIABKXUDAAAAAAAAAAAAAAxIqRsAAAAAAAAAAAAAYEBK3QAAAAAAAAAAAAAAA1LqBgAAAAAAAAAAAAAYkFI3AAAAAAAAAAAAAMCAlLoBAAAAAAAAAAAAAAak1A0AAAAAAAAAAAAAMCClbgAAAAAAAAAAAACAASl1AwAAAAAAAAAAAAAMSKkbAAAAAAAAAAAAAGBASt0AAAAAAAAAAAAAAANS6gZuVFUtrqpWVZ8fOgsAAAAAAAAAAADATY1SNxtcX/5tNzJnVT9vt1nOr+t1SFXtO4d546/xtW5XVa+rqm9W1a+rak1VXVBVJ1XVP1TVzTb0Z7OhVNV7+2e67dBZ5quqvlJV1w6dAwAAAAAAAAAAAGBzsXjoADCLNyVZPcvYt/uxo8fO75jk8CSXJDl2wnW/vV9VPT3Jm5Ns09/v/f34LZPs1Y/9c5JdFvwENyGttWurao8klw+dBQAAAAAAAAAAAOCmRqmbzdWxrbVVNzJn2eibfifuw5Osbq0tu+H03857UpK3Jrk4yRNba5+ZMGfvdMVyeq21Hw2dAQAAAAAAAAAAAOCmaNHQAWBTqqod8ruy9uMmFbqTpLX2X0keOOH6h1fVZ6vq11V1VVX9uKpeVVU3nzD3K1V1bVVtXVVHVdVPq+rqqjqrql5dVVtPuGafqvpkVf2in3teVf13Vb24H19cVS3JE/tLzq6q1r9+OmHtbatqWVX9pL/fcf34jlX1gqr6YlWdU1XXVNUFVfXxqrr/hFyL+zU+P3b+Ff35varq8VX19aq6oqouqqr3V9WuI3Pv3Gd/cJKtRnLf4L4AAAAAAAAAAAAAWxI7dbOleVySHZN8pbV28romttauHn1fVX+X5H8nuSzJh5P8Ksl+SY5I8uiq2qu1dsmEW30gXUH8M0kuTfJnSV6U5JZJDhu5/4FJ/iPJ6v74yyR/mGSPJM9I8vIka5McneQvkuyZ5I1JftPf4uIJa/97knsn+Wz/v8/tz98jySuSfCnJif2at0/ymCSPqqpHtdbmU7R+dpJH97lX9M/7hCT3qqr7tNau6fMdneQpSW6b5GUj158xj7UAAAAAAAAAAAAAblKUutloqmrZOoZ3vJHLn1NVq2cZe01r7aqFpcpe/XGdhe5xVXXH/K5Aff/W2k9Gxt6erpz96iTPGrt0qyR/nOTurbVf9/P/Ocl3kxxaVUe21n7Vzz0sSSX509ba98bWv2WStNbWJllWVXdOV+o+prX2i1lib5Vk1yR7ttYuGhv7XpJdx89X1e2TfK1/1j3X8ZGMOyDJfVtr3+/vU0k+mOTgJAcm+Vhr7eI++8OS3Lq1tmwe909VrZxl6K7zuQ8AAAAAAAAAAADA5kapm43ppetx7eHrGDs2yUJL3bv2x9mK0LP5myRbJ3nzaKG7d0SSv0ry5Ko6vLW2Zmz8BTOF7iRprV1WVSckOTLJ0nQ7eI+6Ynzx1tqF88w746gJhe601iYW5ltrP6+qjyV5ZlXdurX2yzmu88aZQnd/n1ZV70hX6r5/ko8tIDsAAAAAAAAAAADAFkGpm42mtVazjVXVqiS3X8fld2itrdrQmdLthJ0kbZ7XLemPXxgfaK1dVFXfSfKgJP8jyffHpnxjwv3O7o+3GDn3viSPSfKNqvpgki8m+Wpr7Zx5Zh116mwDVbV3kmcneUCSP0qyzdiU2ySZa6l7rs+4YK21pZPO9zt4L5k0BgAAAAAAAAAAADANlLrZ0syUlG87z+t26I/nzjI+c37HsfPXtdYumzD/2v641cyJ1tqHqurKJM9L8rQkz0iSqvp6kiNaayfPM/N1rbVfTRqoqoOTfCDJlUlOSnJGksuTrE3ykCR7J9l2HmtN2vn7Bs8IAAAAAAAAAAAAwA0pdbOl+UqSJyV5aJKj53HdJf1xlyQ/njC+69i8BWmtnZjkxKr6/XQ7aD86Xbn7k1V179bapLUX4uVJrkqydPyeVfXH6UrdAAAAAAAAAAAAAGwCi4YOAJvYh9LtKr13Ve23rolVNbpT9bf6474T5u2U5J5Jrsjkwve8tdYub62d3Fp7TpLXJtkuySNGplzXHxe6C/adknxvQqF7qyQPXuA95+q6bqmqjbwOAAAAAAAAAAAAwFRQ6maL0lq7JMnh/dsPVdX+k+ZV1YOSfHXk1HuSXJvk8Kq6w9j0Vyb5gyTHt9bWLDRbVT2sqrabMLRzf7xi5NxF/fF2C1zu50nuUlW7jKxfSV6W5C4LvOdcXZTuvz233cjrAAAAAAAAAAAAAEyFxUMHgFk8p6pWzzK2orW2YqE3bq0dX1XbJ3lzks9V1beSnJLkkiQ7JXlQup23zxu55mdV9fwkb0ry7ar6UJILk+yX5E+S/CDJEQvN1Ds2yW2qakWSVelK5PdNtzv4mel2GZ9xcpLnJnlnVX0syWVJLm6t/esc13pjkrf0z/LRfq29k/yPJJ9McuB6Psu6nJzkz5N8vKo+k+TKJGe21t63EdcEAAAAAAAAAAAA2GwpdbO5OvxGxlesz81ba2/rC8V/l2T/JH+d5PeTrE5yWr/+v41d8+aq+kmS5yc5OMn2Sc5K8tokr+53AV8fr0zy2CRL+0xr+/u/IsmbRu/fWvtUVb0gyVPTlbu3SfKzJHMqdbfW/k9VXZnuOQ9Ntwv4l5P8TZInZOOWut+W5I+TPD7JC9L9d+jkJErdAAAAAAAAAAAAwBZJqZsNrrVWc5iz23zOz3HdVUludO2R+T9PVyqezxqfSfKZOc7dax1jxyU5buzcCUlOmEeW1yd5/XzXHpnzriTvmjB0VP8anXttJny2rbUbzB0Z++ks11yb5EX9CwAAAAAAAAAAAGCLt2joAAAAAAAAAAAAAAAAWzKlbgAAAAAAAAAAAACAASl1AwAAAAAAAAAAAAAMSKkbAAAAAAAAAAAAAGBASt0AAAAAAAAAAAAAAANS6gYAAAAAAAAAAAAAGJBSNwAAAAAAAAAAAADAgJS6AQAAAAAAAAAAAAAGpNQNAAAAAAAAAAAAADAgpW4AAAAAAAAAAAAAgAEpdQMAAAAAAAAAAAAADEipGwAAAAAAAAAAAABgQErdAAAAAAAAAAAAAAADqtba0BkAFqyqVi5ZsmTJypUrh44CAAAAAAAAAAAAbMGWLl2a0795Rn7Tfl3zvXbxxggEsDFV1c2S3Kx/u/XatWuHjAMAAAAAAAAAAACwXhYNHQBgAZ6f5Jz+tef5558/cBwAAAAAAAAAAACAZPc9r1zQdUrdwDR6Q5Lb9K/Tdt5554HjAAAAAAAAAAAAACzc4qEDAMxXa+3SJJcmSVWtWbSo+/uU/RcdPGSsOTtp7Yev935acieyD2FacyeyD2FacyeyD2FacyeyD2FacyeyD2FacyeyD2FacyeyD2FacyeyD2FacyeyD2Facyc3zL72vN0HSjJ/i3Y5/XrvpyX7tOZOZB/CtOZOZB/CtOZOZB/CtOZOZB/CtOZOZB/CtOZOZB/CtOZOZB/CtOZOZB/CtOb+rTVnL/hSO3UDAAAAAAAAAAAAAAxIqRsAAAAAAAAAAAAAYEBK3QAAAAAAAAAAAAAAA1LqBgAAAAAAAAAAAAAYkFI3AAAAAAAAAAAAAMCAlLoBAAAAAAAAAAAAAAak1A0AAAAAAAAAAAAAMCClbgAAAAAAAAAAAACAASl1AwAAAAAAAAAAAAAMSKkbAAAAAAAAAAAAAGBASt0AAAAAAAAAAAAAAANS6gYAAAAAAAAAAAAAGJBSNwAAAAAAAAAAAADAgJS6twBVtayqWlXtO3QWplNVraqqVUPnAAAAAAAAAAAAALgpUuqeclX1z31hu1XVXYbOMy2q6g+r6sVVdUpVXVhVa6rqoqr6r6o6sqp2HjrjbKa5pF9Vy/vsuw2dBQAAAAAAAAAAAGBzodQ9xaqqkjw1SetPHTbL1Lck2SPJqZsi1+auqg5M8rMkL0tyqyT/nuR1SU5Isl2SVyT5WVXtMljIzc9D+xcAAAAAAAAAAAAAG9jioQOwXh6e5A5Jlid5ZJInV9WRrbVrRie11i5McuGmj7f5qap9knwsyXVJDk3y7tZaG5uzZ5I3pSt4k6S19rOhMwAAAAAAAAAAAADcVNmpe7rN7Mz9jiTvS3LLJH8+PqmqllVVq6p9x863qlpRVbtU1XFVdU5VXVdVh/Tjy/s5d6iqv6+qH1TVVVW1qqqO7HcKT1UdXFWnVtXlVXVBVb2lqm5QiK6qg6rqvVX1k37uZVW1sqqeXVU3+C1W1c5V9S9V9eN+/ur+fy+vqjuOzKuqenJVnVJVv+oznl1Vn62qx4/MW5TkrUm2TnJ4a235eKE7SVprpyV5WJJzxvIsraqP9s94dVX9vKr+tap2nZB95rPbraqeXlWn9bnOr6q3V9UOE665Z1Wd0H++V/fP8s2qOraqtu7nrEry0v6SL/ZrtKpqE9a+Y1X9Q1V9t6qurKoV/fg2/ff56f4Zrq6qi6vq81X1yPFcM+v2a4+eO6Rf55Cq2q//LV1aVb+pqk9V1R5j81uSJ/dvzxzJfr37AgAAAAAAAAAAAGxp7NQ9papq5ySPSfKT1topVfWbJM9L8rdJPjiPW+2U5P8luSzdDtZrk5w/Nudfkuyb5MQkn+vXfWWSbarq4iSvSfLxJP+VZP8kf5dkqyTPHLvPa/r7fy1dYXqHJA9Jtyv2/b9fBC4AACAASURBVJL8zcjz/V6Srya5U5KT+rUrye2TPDbJR5Kc0U9/ZZIjkpyZ5ENJLkmya3/Pg0c+j32S3LVf+53r+lBaa2v7rDN5Dkzy0T7DR5L8PMnS/hkfW1UPbq2tmnCr1yU5YOSz2y9dGf/O/bPP3P+e/efSkvxH/yw37+c9K8lRSdYkOTbJQf2zvDvJpDVnvCnJ3kk+leTT6XYnT7rv/E1JTkn32f4q3ef16CSfrqrDWmvHrevzGXNguu/kP9OV5u+W5FFJ7ldVd+t3ik+So/vs9+rXX92fXx0AAAAAAAAAAACALZhS9/Q6NN2O08uTpLX2var6ZpL9qurOrbWfzvE+eyZ5T5KntNaunWXO0iT3bK2dk3Q7fyf5aZJ/SnJFkqWttR/2Y9sm+VaSp1TVS1trF4zc589aaz8bvXG/e/a/JXlSVb2ltfa1fuih6Qrdx7bWnjt2zTZJth059fR0Re17tNauGJt7y5G3e/XHFa216zJHVfUH6T7nxUn2ba3918jYC9OV1d+e5OETLn9Akj1ba2f18xcn+UK67+n+rbVT+3lPTrJdkoNaa58YW/8W6T7ntNaOraod05W6l7fWVqwj+pIk92mtnTl2/tdJbt9a+8XYOjukK9K/rqre11q7ch33HnVQkgNaayeP3OvVSV6U5Cnpiu1prS2rqt3SlbqPnaUEP6uqWjnL0F3ncx8AAAAAAAAAAACAzc2ioQMwf1VVSZ6Wbifp40eGlqfbSfpp87jdNUn+cR2F7iR5+UyhO0laa6vT7Sb9e0n+70yhux+7Ot3O2Nsk2WP0JuOF7v7c2nS7NifdjtbjblAsbq1d01q7dOz0mvxuJ+rRuReOvN21P/5ifN6NeGySP0zywdFCd+8N6XbL3r+qbjfh2pfNFLr7PNemK7Enyf0nzJ/0vL/uP6f5et2EQndaa1ePF7r785ckeVeSW6Tb5XyuPjBa6O69vT9OekYAAAAAAAAAAAAARih1T6eHpNvF+qTRsnWS96craR9SVVvP8V6rxnbTnuQbE879sj9O2j15JtNtR09W1R9W1Wuq6rtVdVlVtapqI/e4zcj0L/X3eVFVfaaqnl1VS6tqqwnrvS/Jbkm+X1WvrqpH9LtOj6v+2CaMrcuS/viF8YG+pP3l/u19Jlw76bM7uz/eYuTcB9OV0j9eVcdX1ZOq6k7zzDnu1NkGquruVbW8qs6oqitHvos39FNuM9u1E8z1GddLa23ppFeSH22oNQAAAAAAAAAAAACGoNQ9nf62Py4fPdlauyjJiUl2Tre79FycN4c5l0w4d+0cxn5bLK+qHZN8PckL0+1GfXySVyY5Or/bqXvbmfmttd8keUC6Xa2X9nO+keS8qjp6rLT+3CTPSXJ5khcl+c8kF1bVJ6rqziPzZoro1yubz8FMQfzcWcZnzu84YWz1hHMzn89vC+qttVOT7J2uOP6XSd6d5KdV9aOqesI8886Y+N1W1QPSfRd/leTHSd6W5OXpvotP9NO2nXTtLG7wjCM7v08q4QMAAAAAAAAAAAAwYvHQAZifqrpVkoP6tydU1QmzTP3bJB+Zwy3nu2v1Qj0tyR2SHN1aWzY6UFUPTHL4+AWttV8keWpVVZK7pduh/O+SvCTdHyS8uJ93XbrS95uq6o+S7JXkfyU5OMndq+rurbWrk3ylv/W+VbVVf91czBTXd5llfNexeQvSWvvvJAdW1bbpiuyPSPIPSd5fVb9qrX1+vrec5fxRSbZPsl9rbcXoQFUdkbn/QQAAAAAAAAAAAAAAG4BS9/R5cpJtkqxM8u1Z5jwmycOq6g6ttTM3WbJ1m9kx+6MTxvZZ14WttZbk+0m+X1UfT3JWumL7iyfMvSDJx5J8rKpOTlcEv0e6z+tLSX6U5K5JDk1y3GxrVtWiJFu11tYk+VZ/et8k7xybtzhdiTxJvrmu55irvoB+SpJTqur0dLuaPzbJTKl7poy+0F2w75zk4vFCd2+d38UGsL7ZAQAAAAAAAAAAAG5yFg0dgHl7Wn98VmvtaZNeSd6WpEbmbg5W9cd9R09W1X2SHDE+uaruUVW7TbjPzv3xin7etlX10H4379Hrt06y0+jc1traJM9Icm2SN1fVX49f1197tySfS3Kb/tTHk1yc5AlV9YCx6c9Jcsckn2+tnTUh75xU1d5VtcOEoes9b++i/ni7BS63KslOVXXPsQxPTXLAAu85V+ubHQAAAAAAAAAAAOAmx07dU6Sq9k1ylySntdZOXcfUdyb55ySHVtVLN0W2OTg+yT8lObaq9ktyepLdkxyYbmftx4/Nf1iSY6rqlHS7a1+Q5Lbpdqxem+T1/bzt0+1gvaqqvpbk50m2S7J/kj2S/Edr7YczN22tfamq/iLJe/rXi6tqRZJfJdkhyX2T/EmSy5Nc2V9zWVU9JcmHk3ypqj6cbrfwpUkenuS8JE9fz8/n+Uke3mc5I8llSe6e5JFJfp3k7SNzv9h/Bq+uqnv042mtvWKOax2brrz9lar6UJJL0j33Xkk+kuQv1/NZ1uXkdL+Dd1TVR9I95+rW2ls24poAAAAAAAAAAAAAmzWl7ulyWH88bl2TWmurqurz6YrNj97oqeagtfbLqto7yWvSlYcPSFfWfla6UvZ4qfuz6crHf5quyH3zJOcmOSnJMa21U/p5lyd5YZL9kjwoyUFJLk3ysyTPTPKuCVlOrKo79Ws/Ml2J+eb9dT9K8pIkb2+tXTByzSeq6sFJjuyz75CuzP3WJC9vrf1yoZ9N71/TlbP/JMmD0/3b/EV//g2ttZ+PZPlhVT05yT/2z7BdPzSnUndr7TNV9egkR6X73K9Lcmq6z/CO2Yil7tbaZ6vq+el+y89Nsk26Ir5SNwAAAAAAAAAAALDFUuqeIq21JyZ54hznPnzk7b8nWTZhTt3IPQ5JcsgsY8sm3bMfW55k+YTzP0jymFmWq7G5P0zyvHXl6+etSfK6/jVnrbWLkry8f831mq8n+fM5zj0ks392K3LD5/1cks/NI8t7k7x3vmuPzPlkkk9OGPpyJn93u004t3zS3JHxib+v1toxSY5ZVz4AAAAAAAAAAACALcmioQMAAAAAAAAAAAAAAGzJlLoBAAAAAAAAAAAAAAak1A0AAAAAAAAAAAAAMCClbgAAAAAAAAAAAACAASl1AwAAAAAAAAAAAAAMSKkbAAAAAAAAAAAAAGBASt0AAAAAAAAAAAAAAANS6gYAAAAAAAAAAAAAGJBSNwAAAAAAAAAAAADAgJS6AQAAAAAAAAAAAAAGpNQNAAAAAAAAAAAAADAgpW4AAAAAAAAAAAAAgAFVa23oDAALVlUrlyxZsmTlypVDRwEAAAAAAAAAAAC2YEuXLk3WfD8rv3tVzffaxRsjEMDGVFU3S3Kz/u3Wa9euHTIOAAAAAAAAAAAAwHpZNHQAgAV4fpJz+tee559//sBxAAAAAAAAAAAAAJLTT9t+QdcpdQPT6A1JbtO/Ttt5550HjgMAAAAAAAAAAACwcIuHDgAwX621S5NcmiRVtWbRou7vU/ZfdPCQsebspLUfvt77acmdyD6Eac2d3LSyrz1v94GSzM+iXU6/3vtpyZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3IPoRpzZ3cMPs09xmmJfu05k5kH8K05p5xejtjwdfaqRsAAAAAAAAAAAAAYEBK3QAAAAAAAAAAAAAAA1LqBgAAAAAAAAAAAAAYkFI3AAAAAAAAAAAAAMCAlLoBAAAAAAAAAAAAAAak1A0AAAAAAAAAAAAAMCClbgAAAAAAAAAAAACAASl1AwAAAAAAAAAAAAAMSKkbAAAAAAAAAAAAAGBASt0AAAAAAAAAAAAAAANS6gYAAAAAAAAAAAAAGJBSNwAAAAAAAAAAAADAgJS6AQAAAAAAAAAAAAAGpNTNBldVy6uqVdVu63mfQ/r7HLJBgrFgVbWiqtrQOQAAAAAAAAAAAABuipS6b4Kq6p/7MnSrqrvMMmdZP77vjYy3qnrWLHNmStev2IDx18tcC+VV9ftV9Zyq+kJVXVBV11TV6qo6tapeWVV33DSJ52+ay+439rsDAAAAAAAAAAAA2BIpdd/EVFUleWqSmV2VD9sAt11WVTefx/wjkuyR5JwNsPYGV1UPSPLjJG9MsnuSTyf5lyTvTnJVkhcm+VFVLRks5ObnSem+UwAAAAAAAAAAAAA2sMVDB2CDe3iSOyRZnv/P3nmGSVKVbfg+G2ADOS85ZwFBJGckSgYlB0EkKFk/SQIiKiqIBAVMgEjGAKKgoEQRBUUQAQVZkaACEiUs0PX9eN+ya2urZ6ZnusLpfe7rOlfPVJ069dTbT1c4dQJsCewTQjguSZIpwyzvMWBJrKHz8UPZIEmSZ4Fnh7m/UgkhLAvcBMwEfBo4I0mSd3J5FgNOB7ppyN7XJEnyZN0ahBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIfoVjdTdf6Qjc38T+D4wF7BDNkMIYTJwkv/7qxBCkqaC8s4BngGODCEsOBQBIYSLvLxFc8tDCOHwEMKfQwhvhhCeDiGcG0KYNYQw2XV1KnOjEMKtIYRXQwivhBBuCCEsl8uTAPv4v09kjitb7jlYY+3TkyQ5Pd+gGyBJkieSJPkQcHeu/KVCCJe47ikhhGf8/6UK9J7s+94whLBzCOG3IYTXQwj/CSFcEUJYoGCbxUMIF4YQHgshvOF5HwwhnB9CmNPz3Ap81zf5bva7S+Od2/fuIYR7QgivZeMQQtg3hHBtCOFvvq9XQgh3hRD27BD/W/P+8PIT398q/p285Md5Wwhh7Vz+yQzdd0IIIYQQQgghhBBCCCGEEEIIIYQQQgghhBDTDRqpu48IIcwLbAv8JUmSX4cQXgGOAg4ErsxkPQvYHtgAuBiYPECxrwMnAt8GTqPdaHo4nAccjDUSvxCY4nrfD4wF3u6w3QeB7YCfAecDywNbAauHEJZPkuR5z3cKdlwrA18DXvLlL8H/RuDeFHgT+NJgYpMkeSv9O4SwOnAzMDNwHfBnYFlgD2C7EMImSZLcW1DMIX6M1wG3AWsAHwZWDiGsku4jhDAJ+B3W4PynwLXAOGzU9b2Ac4EXsBHYX/J4/Bi4P7Ovl5iao4EPANcDvwJmzaz7hh/D7dio6nNiMf1eCGGZJElOHCw+Gd4HfAprBP8tYGFgJ+AWP8ZHPV83vhNCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYSYblCj7v5iP6xx9EUASZL8KYTwe2CjEMKSSZI85svPCiHMhjWuvShJklsHKfci4HBgzxDCV5MkuX+Q/NMQQlgPa9D9F2CNJEnShtbHYY2l5wf+3mHz7YHNkyS5JVPeF4BPAx/BG2gnSXKyj1a9MnBWkiSTc+Ws65/3pfsfovYAXII1uN4zSZLvZ9Z9GLgCuNQbmLdym28BrJ4kyYOZbS4DdsMaZl/li3cG5gCOSJLka7n9TwRafowXmRy2A36UJMlFA0jfGFgrSZI/FKxbMUmSx3P7mQFrOP/pEML5SZI8PUDZWbYG9stqCSF8DGuAfzjWsH04vhNCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYSYLhhVtwDRG7zh8QFY499LMqsuAtJ1w8IbKn8K88tXhllMOsL3adkG1UmSTAGOHWTbK7INup0L/fP9XWiY5J9PdbENwNrYqNx3Zxt0AyRJciVwJ7AM7UbjWc7ONuh2vumfRdrfyC9IkuS/SZJMs3wIXNihQTf5Bt2+bAo2mvoYYJMu9nNXQePy7wDv0N33MyAhhPuKEvbdCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQkSLGnX3DxsDSwC/yI2wfBkwBdg3hDB2uIUnSXIT8HNgkxDCVsMo4r3+eWfBut9gDYA7cW/Bsn/45+xdaAj+mXSxDcCq/vnLDuvT5e8tWDdU7dcBrwHnhRCuDSEcGEJYwRvrD5ffdloRQlg4hHBeCOGREMLrIYQkhJAA13qWBbrYzzTHmCTJ28C/6O77EUIIIYQQQgghhBBCCCGEEEIIIYQQQgghhJguGVO3ANEzDvTPi7ILkyR5IYRwPbATsB1wzQj2cQxwP/ClEMJNXW47q3/+K78iSZJ3QwgvDLDtS/kFSZK84+2dR3eh4Rn/XLCLbaCt/dkO69PlsxWsm0Y77Qbs/9OeJMnfQwjvB04GtgB29FX/CCF8JUmSs7tSbPyzaGEIYXGswffswB1YY/2XgXeBRbFR1WfsYj9Fxwh2nN18PwOSJMlqRct9tO5Vi9YJIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCxIBG6u4DQghzA9v7v5enoy5nRl/eydcdWFzC0EiS5EHgYmAF4CNdbv6Kf86bXxFCGA3MORJtQyQdJfx9IYRZB8w5NS/753wd1k/K5RsWSZI8nCTJh7FYvA/4NPYb/VoIYf/hFNlh+VG+j/2TJNkwSZLDkiQ5MUmSk4FuG+sLIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCiBGiRt39wT7ADMB9wLc7pOeATUMIi/k27/pntyMpnwC8DnwWmNjFdn/wz3UL1q1J70aN73hcSZI8AdwMjAM+OVhBIYR0tOpU+4YdsqbLfz9UkQORJMk7SZLclyTJ6cBuvnj7TJbhfncpS/rntQXrNhhmmUNlpNqFEEIIIYQQQgghhBBCCCGEEEIIIYQQQggh+g416u4PDvDPQ5IkOaAoARcAIZP3Bf9cuJsdJUnyDHAGNmr1EV1seol/Hp8dJTuEMAPw+W40DMJgx/UJbNTwY0MIR4cQpmlMHkJYOIRwBbCWL7oLeBRYN4Swcy7vzsD6wF9ojwTeNSGE94cQphnFnPbI5q9nlg3ru8sw2T83zGnYnLY/ymKk2oUQQgghhBBCCCGEEEIIIYQQQgghhBBCCCH6jl6NjixqIoSwIbAM8GCSJL8dIOu3geOB/UIIJwG/AlrAF0IIKwIvAiRJ8rkh7PZLwIG0R3welCRJbgshXOjbPRRCuBZ4G9gGeBl4xvWMlFuwUbi/GUK4BngNeClJknNdxyPeePla4CvA4SGEW3z/E4GVgXWABDjdt0lCCPsAvwCuDCH8GHgEi/v2wKvA3kmSjET/7sChIYTbgMew72MJLD5vAWdl8t6NNfI+IoQwB/AvX35OkiQvD2FfXwf2A6727+FpYEVgC+Aq4MMjOI7BGInvhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIfoSNeqOn4/657cGypQkyeQQws3AB4BtkiT5oTdUPgY4BBjnWQdtXJskyWveMPz8LrUejDWG/hhwEDZq8w+B44CngMe7LK9I200hhKOxuBwJzAD8HTg3k+c3IYRlPM+2wNbA7FhD6cewkcgvTJLkicw294QQVgdOADbFGls/D1wOnJokyaMjlH45MCOwNrAqMB5rbH0FcEaSJH/KaHkxhLATcBLWOHuir7oUayA/IEmSPBBC2Aj7rrfCzgN/BHYEXqLERt1Jkjw8XN8JIYQQQgghhBBCCCGEEEIIIYQQQgghhBBC9Ctq1B05SZLsAewxxLyb5f6/FGsIXJT3ZODkAcq6ALigw7p9gX0LlreAr3r6HyGEpYCZgIdz+S8CLhpAQ+iw/EzgzE7beZ7XirQMss2jwF5DzHsyHeKXJMlkIOSW3QPc04WWG4Ebu913Js+vgY07rJ4mrkmSbFiw7NaivJn1i3ZY3tF3QgghhBBCCCGEEEIIIYQQQgghhBBCCCGEENMjo+oWIKYfQgjzhRBG5ZZNAM7yf39YvSohhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIepFI3WLKjkC2C2EcCvwLDAfsAmwIPAz4Or6pAkhhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIUQ9q1C2q5BfAysBmwBzAO8BfgLOBs5IkSWrUJoQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCFELahRt6iMJEluAW6pW4cQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEE1iVN0ChBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQYnpGjbqFEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBCiRtSoWwghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIWpEjbqFEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBCiRtSoWwghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIWpEjbqFEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBCiRtSoWwghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIWpEjbqFEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBCiRtSoWwghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIWokJElStwYhhBg2IYT7Vl111VXvu+++uqUIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBiOma11Vbjr7//G68kL4Zut1WjbiFEdIQQZgZm9n8fGj9+/GzLLbdcnZKEEEIIIYQQQgghhBBCCCGEEEIIIYQQQggxnfPwww/z9hvv8HYyRY26hRD9TwjhZOCkzKJ3gD8BrR7valn/fKTH5QKMAuYF/kXvdUO82svUDfFql1+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KkV+KidkviwKvJEmyWLcbqlG3ECI6ciN1zwv8HlggSZJneryf+wCSJFmtl+V62fMDT1OCbi8/Su1l6vbyo9Quv3QsW34pLlt+KS5bfikuW34pLlt+KS5bfikuW34pLlt+KS5bfikuW34pLlt+KS5bfikuW34pLlt+KS5bfikuW34pLlt+KS5bfikuW34pLlt+KS5bfikuW34pLlt+KS5bfikuW34pLlt+KS5bfikuW34pLlt+KS5bfikuW34pLlt+KS5bfikuO1q/jIQxdQsQQohuSZLkVeBVgBC6nqFACCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQolGMqluAEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCTM+oUbcQInZeBU7xz5iIVTdIex3EqhukvQ5i1Q3SXgex6gZpr4NYdYO010GsukHa6yBW3SDtdRCrbpD2OohVN0h7HcSqG6S9DmLVDdJeB7HqBmmvg1h1g7TXQay6QdrrIFbdIO11EKtukPY6iFU3SHsdxKobpL0OYtU9IkKSJHVrEEKIRhJCuA8gSZLV6tbSLbFqj1U3SHsdxKobpL0OYtUN0l4HseoGaa+DWHWDtNdBrLpB2usgVt0g7XUQq26Q9jqIVTdIex3EqhukvQ5i1Q3SXgex6gZpr4NYdYO010GsukHa6yBW3SDtdRCrbpD2OohVN0h7HcSqG6S9DDRStxBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQtSIRuoWQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEKIGtFI3UIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCFEjatQthBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQNaJG3UIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCFEjatQthBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQNaJG3UIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCFEjatQthBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQNaJG3UIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCFEjatQthBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQNaJG3UIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCFEjatQthJjuCCGEujV0QwhhXAhh1xDCnHVrGS6RxnyrunWMlJjirpjXg8d9Pf87yvvCSGMur1eMvF49/eD1SGMetc9Bca+DSGO+mv89um49wyWmuPfDOR3iijno/FIH/eD1SGMetc8hrrj3g88hrphDf3g90pjL6xUjr1ePvF49/eBziCvmEHesYyb1Scz1L7ERe8xjO7fkiTHuscY8Zq/HGvOUGGMO8cZdXq+PGGOeRTe/Qoi+J4SwVQhh3xDC9iGE2TLLG38ODCEcCrwMnAlMqlnOkAkh7BxCOD6E8IkQwirAWF/e+It+COEQ4FXgwhBCNDGHeOMeecy3DyEcFkLYJ4SwEH5vFcn55RDgv8ClIYQZkyRp1a1pKPRBzOX1ipHXqydWr/dBzKPzOSjuddAHz0cvAeeHEEYlSfJu3ZqGSqxxj/WcDjq/1EEfxDw6r/dBzKPzOcQb91h9DvHGHOL1eh/EXF6vGHm9euT16onV5xBvzAFCCEcD94QQ5qtbS7eEEObPxziEZr+zSwkhHAPcARBZ/YtiXgMhhLkAkiRJ6tbSLSGEI0IIP4C44h55zKP0euQxj9LnEH3c5fWKidnrecbULUAIIcoihLA28HVgeaAFzAA8CFwGnN7kypYQwibAucAywLXAFcDfahU1BEIIqwMXAisA7wIz+qorQgiHJ0nyXG3iBqEg5lcCL9YqaojEGvfIY74mcD52fkmwBvTPAZcDR0R0frkGuLpeRUOjj2Iur1eEvF49sXq9j2Iejc9Bca+DPno++gFwKVanNaVOXUMh1rjHek4HnV/qoI9iHo3X+yjm0fgc4o17rD6HeGMO8Xq9j2Iur1eEvF498nr1xOpziDfmMFXclwJuBWYB/lmnpqESQtgIOA5YEJgYQrgeuDZJkl82vYFULu63hxAWSZLk7zXLGhTFvB5CCBsCxwDzhhBmwK5L1yVJcn+wARliOMcsA1wfQpiU5PahjwAAIABJREFUJMmzNcsalD6JeVRe75OYR+Vz6Ju4y+sVEbPXO5IkiZKSklLfJWBj4BngAeCTwI7AF4A3sBfphwIze95Qt96M7vmB61zjPcBHgYXq1jVE7SsBDwFPAIcA6wBbYA0WWsD3gfc0MOYLZGL+25hiHmvc+yDma2KdLB4FDgM2Aw4EnvVj+kJ6PE2JeUHcfwccACxYt67pKObyej1xl9erj3lUXu+TmEflc8W9Nu2xPh8tCPw4xpjHGveYz+muX+cXxXw4MY/K630S86h8HmvcY/Z5rDEviHtUXu+TmMvr9cRdXq8+5vJ69TGPyuexxty1LAxcT/td6f4xeB0IwHjgi679AeBnwB/8/zeArYAZmxbzTNx/ElPcFfNatU8EznLtjwJ3AU/5/08Dq9Stscu4N/7c3ocxb7zX+zDmjfd5n8ZdXq8+5lF4fdBjq1uAkpKSUhkJG9n6v8BWueW7YD3QnwP2BkbVrTWjbUHgl36xORtYqW5NQ9Q9yj9PA94G9sqtX5125cu3gRnq1pzRtjTwZ9f22VhiHnPcI4958M9vAG8CO+XWb4pVFL0GnAiMqVtzRtt7gRc87kfHEvfIYy6v16NdXq9ee5RejzzmUfpcca9df4zPR+t4vFtYg+ioYh5j3GM9p7t2nV8U8260R+n1yGMepc9jjnusPo855q4tSq9HHnN5vR7t8nr12uX16nVH6fOYY+7ajvKYT3Zt0cTd9W/gvvkh8F5fNgY42Y/rcWDXunUW6D7e9f0V+ExMcVfMa9P/QT+HXJKJ+7zAeX5c9wHr1K2zQPdpGV9ME3ca1vC/T2Ierdcjjnm0Po887vJ69bqj9vqgx1e3ACUlJaVeJ6wX0b+AX2aWjcn8/SngVeDXwPvr1pvRFYAjgJeBszPLFwLWxXrPnwZsAyzp6xrx8t+13A78h3av/mzM18FGk34T2C893gZoHoX1OHsH+HRm+fxYo+h9gMNd/9xNi3mMce+TmP8ZeASYqSDmu2G9Fp8Atm5CzF3DaOBHflO7d2b5JGy0912AXYH3AOOaojvymMvr9WiW16vXHLXXI4151D5X3GvRHuvz0Rjgj8AUYNvM8nmxKfS2BTYBFsusa0TMY4177Od016Pzi2I+FM1Rez3SmEft8xjjHrvPY4y5a4ja65HGXF6vR7O8Xr1meb16vVH7PNKYzwr81GN+Qm5dOtLyAllvN9Dn6Wxja+WWzwCcBLyOjX65WhNi7hrmwkblbAEH5taN8c/Zc8tr162Y16p/FPZ++jVg+dy68cB3/diuAJZoin4/f7+TP69n9aXn86aliGMerdcjjnm0Po887vJ69bqj9vqQjrFuAUpKSkojScDYgmXLA28B9+eWpyMbLwRc5if4zwITGnAcqbbFsdGVX8F6ym8KXOX/tzLpL8CKTbhYuu45gDuAlyiYPhx7cD7Itd8OzNcAzaP9c2Wsschz2GgXmwJXAy/mYn4nME+NeufKf9+xxT2mmHf6bWHTt0wG/lGU37+TL7j+S/I35zUdS/qgsL7H+Cm/Ad/Y4/58JuZvAJfilbw1aJ1mv5HGXF6v51jk9eqPIwqvy+f1+Nx19pvXGx13OrzIJM7no9Tr23lc7wAmYFNFXwn8OxPz54FTqfElOn3wXBrLOX2g7zjS80s05/U+PKc32uvyue5fRngMUfg8G8PYY+6aovF6P/jcNcnr9RyLvF79ccjr1R9HND53ndF7nfaz8ubAk9hI4gGYDdgaOBMbxOgprLH9x+rUW6Tf043A01gD9VF+DGnMFwO+5zE/g4K6hBrjvgdWP3G7/z8bsBXwRf8uHgQuBraoW7NiXrv+AMwC/Al4MPNdhMyxrQrcis1edxh+HatZd3otPTI97/n/swNbAKcAd2Pv078GvKduzX0Q82i9HnHMo/V55HGX16vXHbXXh3ycdQtQUlJSGk4C5sYe0r5YsC5gvc//A6ybLsvl2QF7wPsDsELF2mfxC9+iwKx5fcCHsEYKDwD/wBrsnoRVWuwJ/MwvTL8CVq5Q9wRgTrzxcIHu611XOiL0qNz2CwM3YxVc+1Qc85mwRhWLAPPn9WHTub2NVXZOxirpTgV2x6bVu8uP7Wp8lIsKtc8NXAfcgPd8y61vZNyBmYGlsJEUx+S1NTzm493vM2SWZb3+G9e2bX6d/78GVrn+D2CzirVPdJ/PA8ziy0Zn1p/h2n+GTUPzInA68HFf95CvP79i3XO7x79DQeVxw2Mur8vr8nrSXK/L59X73LXF7PWZgPnSmMcSd2AcXtmWWZa+wGr689EErAPjrLQr47Lnl2s9plcCf/eYn4lNw3wp9kK3BZyW37YC7VE+lxLpOd216byu+5e+97p8rvuXLnVH6XPXJq/rnC6vNz/u8rq83vdej9Xnri1mr+e1pPUBAfiy6z4F+CT2nvQ1P56/0W5QfyI1N9LNeXwU1oCoRbseIP/ObnOsbuNRYP06tefiPsrPGy3gUOAT2MzS/wUexmYiS+N+UNF3WLLOeYGdybyjjjjmaSO5Rse8QHfW62OAx4B38bYKBb/pj/pv91Zg2QbEPfX6aOBe1743cIzH/Q2sjvFlj/nTwIez21akc15g44LlMcY8Oq/L55VqldcLjq1CzfJ6BKl2AUpKSkrdJqyB8xu0GzuPy62fATgHm6b7KDIP9OnFB+uhk15Q08qM0l/+A8djPcxfwSogbgc2xKcN8zxzARe4tquY9gF1fuDnvv6oKi70fvG7B2uU8DTwFWChNN7++WHXdB3Fo0aPAQ7Beqd9mYoqWrAKnz9gIye8jjWWXzeXZ6FMTK8oiPliWGVdC9gxf2wle/1N4AWs8mruzLr0RqVxcXefP46NGPKix3TFSGJ+JHCb+/0RrLfhvL4und7vk67rbGB8QcwnAF/yPIf6sirOL0e77qf9HHMjflNN+wXA0thI/y3g8oK4vwe76W0Ba1QR94zPXwROxju7ZOPW4JjL6/K6vN5gr8vn1fu8D7x+HFa59iTwDPZyduFcnsbF3b19I9aR7zfYS67ZUr/Q7OejI7FRuP+KnWPOp/2ckY68/V5sxOsWNrrSLLkytqRdGbpUxV6P7rmUSM/pGb/ovK77l772unyu+5fpwefyus7p8rq8Lq/L602Je6w+7wOvH4CNEn4csAGZBt3+uQpwH+1n/W8Ak7BOD3PSfi/2GrBp2Xpz2rfHGg3tiQ0KkGpO35Ue59pOz22X5psT+DrWOeOIKryS0bArdp45Aas7GuvL08/1mXpmtG8AC2LvrZd0vS2scdoSFXr9M77f3wOLZJanvmlyzPcBPo017ls2szw7G0DjYu772cr9vi2ZOq+MX87F3j0f0iHuC2OdTt4Ctq9Y+05YY8ojgLUzXkmvR9t7XKdk4r4IsACwOjaYRMu/m4kVev1E3+9vmHrAkfSc3uSYR+l1+bx6n8vr8vr05PURH3vdApSUlJSGmoBdsIqVKcBFwCZ0mKIa2AvrdXM7uakUMheeg/3k/Z0KtM+PNbp9Axth7ivANb7/fwEn5PJvDByLP5xmLkzp556+7e0l694ImwbkLf+8E+ux3wJuyuVdEqtkeRHYq0N5G2KVLHdVEPMPYNOEvAH8FDgPm968hY08kI7YnfphN6zia55crNMbmcN92x9XoH2njNcvxqZR7OT1xsQdqzD+OVaR+EPgQmxE+RZW6bl3Ln+TYr4p1ohrCjbSwwMesxZwWcHv4gmsV/8HOpS3s2/7kwq0b451uHgDa8x1MXCT7/+OTL7U64cBp5EbdYR2peOpvu23Sta9M0M/pzct5vK6vC6vN9jr8nn1Pu8Dry+DjTDwJjby1lXY/WIL+B25UXyaEndgM4/hFOBZ2qNVvQF8JZe3ac9HW7r217FnjB94rFvAdZl8aUXuqWQ6KGZinlaWft23PaUC7VE+lxLpOd33pfO67l/63uvyue5fpgefy+s6p8vr8rq8Lq83Je6x+rwPvL4p1ungDawxU9rg6VJgmVze/wN+DezWoax0NO+Ls99Vidp3wDqkv0270dBfgaNyntgE65jxW2C1Im3+G24B11SkfXvX+iLtTvMt4AJfn50N4DxsoKztOpT1Pd/2zLK1YzNbp17/LrAFBQNXNTTmm2PnxDczMX8X+CqZDhhNi7mXvyPWOedt19/CBmTYM7t/YH+sXu+HwKIdyjratz+/Iu07uPYXM7/TFvA5Xz8mk/c67NxYOEsB1ragBRxXsde/g9WbjinI18SYR+l1+bx6n8vr8vr05PWexaBuAUpKSkqDJaxBdHqSvQnYA5ivQ97RmW1+7BfSE9ILKTZtV5pnWb9wfStdV+Ix7Ov6zwAmZZZ/xG9cWmQq5oCxFE+VlmpfzC9eD5Mbqa6Hmrf2C999rn8+X75URvOOmfzjsBHo3sUqwRZLNdNujDETNs3FX0vUPdZvOp7EevftT6YBN1Y51AK2ysV0BmCuAWK+ivvlJs/bc79gU87/2PXdht3YTuqQN9XViLj7fo7EevCdmvHLOP//Jf9Otsnkb0LMR2GVlo9hFT77pDHHKjzTKVk2zGwzO/A1j/m3Msc6KhPzefw3enOJ2sdho7A/hVVufiTj9RmxG/IWsGaqL7PdvAPEfWvf7pv+m+mpdmxKyJ/4Pm7BRocY7JzeiJjL6/K6vN5sr8vn1fu8j7z+WffmsbRHEpsdu29827+TdTP56z6/jMEaC092bftgoz3MCOyHvUB/HXhfZptGPB9ho4AdiY2E/mvXm3p9Zmw63BbeADqjbUKaL1de6peP+3YnZZf3WHvUz6VEdk5Pv0d0Xs/HXfcvfeZ1+bx6n/eD12Pzubxej9dj97m8Lq/L6/J6Gdpj9Xk/eB0bKfFxrDH93tgI5+ti7/FafmwrZPLPD2yHN1hPddHu3L2Ib/c0MGcZmn0/cwBnYXUtv8RGSN8L63yRNi5aMpN/QWyAqbexGXj/N0J65hjmxkaGfwqYo0Tt87knX8MGM/g4dn5YHWvs3wLe63nTTiGLubfS0S9Dbv2qvt09lPeed/nMb/FmrP5lnoJ8qbbGxNz3tbHv536s3mtNbICAJ/2YziPTYK4JMff9zOXa/ut++SI2Eu2Nvv8nycxo6N/TnZ5/P6aeoS49vyyS0T5zidonYQ3/33DtRwLrAB+k3RBw8Vxcl3Hd6Tklf47Zxre7jNzsfD32+p20z+u7D+L1xsQ8Vq/L59X7XF6X16cnr/c8FnULUFJSUhosYT20/olNh7BaZnl68RgPzF2w3S7YqNKTgT18WXZasW3Ti2zJ+icCv8AaVqSVD2mFyiis8qIFPE/7Jf/ognKy2nf1ba4tSfOCWIPxZ4DNM8vTi+IBFIw6gE1Dd0M2rjndS3gcflZivOcDrsUqhtYr8Es63dwmQygrq/3jRcfcY+2LYb3IpgAHZpaPwRqyzAmsmB5LZv0yDYj7HB7zZwtukuagPf3ZvfhNXv44aor5kn5++VvWE5nf6LGu4TO57dbzY3kF+HSB9jV9u8tL1n4nNqrl2gVe/yKZRlFdeP0k3+70XurNlL861lnkFaZ+GTHavT4z3jkht936dcdcXpfX5fVme10+r97nfeL1+bHRfP6cWZZ6fXFsqrYWNstOei8/mNfLPr+siD07PAJsULD+HN//flltNOD5CFgZG2nuVvwleeoX//wu8CqwwBDKymr/mms/pkTt0T6XEuE53feh8/q02nX/0mdel8+r93nsXo/R5/J6PV6P2efyurwur8vrZcU9Vp/H7PWMJ9KRtbfLrV8FmzFtSBoy39V7scbKpc1ojDXmPxHrpPBdMo3Off1ZrvvM3PKdsHqAx/DBsbAGxtlOAg8B9+W/jx5qn91j/iJWZ7Jibn36G91niOWl2reg3PfTy2KzMLewBtpLDZA36+MmxDxbt/U6udHxsRmm78Aanw96rqgq5r6PiX7+exmrC10us2422gOmHZ3b7nCsAeBd+Dk1F/cFsWvFT0vUPi/WyeLfwJkD/E43H2J5qfaP+Hbnl6R7DY9NCxu8bZkB8ma93oSYR+l1+bx6n/s+5PVp4y6vd9YerddLiUfdApSUlJSGkoDPZS8sWCPWA4Ar/IT+R6zxwvqZbSZgD9v/xXpObZ1Ztxw2ytq/gJVL1j4am17jn2R6a+fyXOvH9zX/PzvVVcjlXQur5PsHsGqJum9l6sq4bI/mTVzvyVm9nmdtpr4xm93XLYtNo/JW9rsoSftmwMSC5WtiIwHciY2KXdgLi1ylKDZawBNYA5SON5o90r4F1kjnamABYCGs19wNWAXVc9jIBR+jXbk7uu64A7NgI4H/HrsZHJNbPxvW87IFHJ/3dl0xxypy/sjUo29mde3vmg/OeX0ssCfwH1+/V2abZbFz0yvAOiX7ZdcOXl8XG6HiBj/Gaaak6xD3DbHz4gPAQiXqPhAbLear2AgoiwMHYVP6vOTf/bVMPRvADA2Jubwur8vrDfW6fF6Pz/vA6wtjL8+v8/9nzK1/D/bS9B3ggCF4vfS4Y89CvwNWKdJBe9rnnXNeH08zno8O7eD1jbH74MuYetSw/PNQPuYfwCoo76FgtLoea4/yuZQIz+m+H53Xp/6/9POL7yfmc3p0XpfPdf8yPfhcXtc5XV6X1+V1eb1JXo/V533g9XuwZ/cF/P8xmXXLY+/uWrQ7Q6cNqdL3kvm4n0SmIT3lNNKdC2uodW1O7wz+uQH27u3MnObZsbqZd7EG9cvmyt3RtV9YYrwnAhdjs9NN42XgK65h6cyykP+7IO5p4/xjy4g7Vodyivv8/zLLF8c6KBzu6zcnMyAA1gmm1pinHsDO6X+hPThE9l3uVlg95PNMO6N0LTH3MpfC6j6/R2bguYy2j3hsj/L/00Hg5vdt3sEGxFg4V+7erv1LJWqfFZv9+qQOXv+u/44LB5DIxD1f/3iBaz+oJK/PClzicd09s3wRrBHsx4CDsQ49s2XW1x7zWL0un1fvc3ldXp+evF6K/+oWoKSkpDRQol3RswL2EPYisD02hXUL63H7e6zCpIW9KF89s91cwPG+7kXgSqxnTzq9x+lY44Yyp86bFZvG4iX84TijL/1cwvW08AfNgov7EsBHsans3vLjGlfCRT69mC/UKTa0Rwo/tEMZ29KuIPoL1lDh9/7/hZQ3jUj+4pwey9zAvlivshZWefQY8CtgB7wCr2D7xbHKx3ux3ndHYZWOZfpldqxC7i2/Wfmha34Qm34unYquBRzD1De3tcQ945eHscYs6Ygh+XimnQH+hk9BU2fMM/5YzH9L03SmoD2qyQ4F24+i3avvTawn5uXurxZwNlZxVob2wbz+W9dwG9ap5DLswWiaWQAyMTgAa7T2KvbwNLrX2jNxXRirCH0Ne1hLff4wcDs28mjq851pT5c3uq6Yy+vyurzebK/L59X7vI+8voLvezK5yjb/ewztl9G/pPPUxlXGfRQ2Q85Ypq6US58t0kbd2VHH0u9qTmp6PmLa55s03vNgU+Pd7xp+5n4/g4JRxjLbL+Ix/6Mfyz5Q2jTXUT+XEtk5PecPndd1/9K3XpfPq/d5P3g9Np/L6/V4PXafy+vyurwur5cR91h9HrvXsef0WYCbsdmBCztjY/UCLezZeqai78yXTQKO9uO4k1yDox7qTp/n98Y71TNtvcYOrvnLBdsvBHzb1z8A7IGNLn4AVv/xJJlZwEryy2wF6+YDjsAaRP0EG2hqY7yheqffjMf9U1hDr58D85Soe2Xgbo/R+4HtsLqi1zP+Tt/1Lpz7fdQS88wxLIy9n/1rh/UTgc+4xh9kfqPTNEKrIuaZfY3xOC2e83+q62Ou+VMF267uXkrrTtfD6s/281g8Cixfku7/1bsVrMvG7yJs4LfCWRiY+jo2P+06vB/g1+aSdG/svvyz73cn7N3+qxmfv+XxHZfZ/v11xTxmr8vn1fpcXpfXpyevl+a/ugUoKSkpDTUBn8Ae0ltYb6fdgZmwRrCTsB7HLb8BmDO37ceBX/vNwL+xCpntK9R+oWs72f8vanxxruc5NbNuDPZA/VOsYuh1rOKu1JGuBziO9EL/Vde61gB51/Lj/it2g3ZXlTHP6BiXuTF50n20q8f7KeAF4GOZ/BOwStJrsEqDNzzmW1aoeQ2PWcs17oFVdI7z9cdgDUYex3v8NSHumRu8j2e9nVk/I+1p9A5qUswHOKa0N+KyA+TZEfgR1gNzMlb5W4fXZwb+z+P7D6zi/lCP+TvYjfYHM/lnxUaSuBirqH7TPbVFRXp3xM7lLWwElN3dIzP5uS/tpXoPsFKTYi6vy+vyepxel8/l9QG0px3/dvX/8y96F8U6A76Qi/ssdce94FhGYy+6XgPmHyBfrc9HGR1zAF/IeP3TWMfGX/myu4H3ZvLPCayDTRt4Sybmm1WoOcrnUvrsnO7adF4vT2/M5/S+8rp8Lq9PDz6X1+VzeV1el9fl9bq8HpvPY/Y69ozcoj2r2Ojc+pk9pi1g39y6tHN7Oir521gHhtVr8nf6rnQP17tTh3xjsc4B6WBMr7ivHgM2rVDvKE9rYp3Mp2Az/96GjdTZwhr5L5vZJj3GRbEOIz/wuP+GTD1NiZoPwuq27sHq45723+e2WKf+tBPG1cBSTYo57UELNkvjn1u/PNbo/Dky73gbEPOiEVFTTcf4Ma3XYdv5Mr/flsd/CvaueqOKvT4aa4R4uX/3//LzRcvj+VVgjoJjXBDr4HOt57uT3Dm0JM2fd22/wM7NT2H1o3v6Z9pZ52xg1ibFPEavy+f1+Fxel9enJ6/3NAZ1C1BSUlLKJ6adXi6dvmJ+P+leDSziy7I9m+YBHvIT+Ca+bIbM+nHYCGllTmudr4RIe/qvmrngTeqQdwPsAfUypu6Bth02mtut+FR1ZeseLB9WQfgo3kgBph2JIfs/PnpEXdqBbfAK0dzynbDp3n4GzOvLZsQaaryKNbiYZrsS/ZLeZEzAesrfCKxQsH424Dz31Im+LP+7KS3uBftKp5rb0jXdi/egy3ljlN88TQG+mN2+wphPE6cO+dKbxEewSqO0QX2h1z3/BAaopK5CO1bhfGTB8qOxESPPp91DdHZsVMj/Ar8DDqtId3pOnwO70b4OWLJguzmxqS5bwD6+bGxmfR0xl9fldXm9QV6Xz6v3eQftMXs91X6Q67oGrzDMeWJG4GTPc0hmeV3nl44jZ2H3ic8CNxblz/m+iuejoXj9dHKjQmAv4c7BKuqOyyxfEHteegOrTD2iBr806rk0H9MC3Y09pw9Be2PP68PRTgPO60PQHfM5vbFe79YrGZ26fylPe2O9ztQDQUTl80G0N9rr3WpvitcH0d1YnxdoiMrrg2hvtNe71d4Urw+iW16X1/vO5x20R+l12u8V0wbQv0j9kP8+aI/WfW7GO+Npz6D2ItYI7Niq4j6Idy703+VSBevS4x4PvA/rPHBa+p1UqT3VgzWaexGb4W12rJPC0lg9y7vYjGnpKOmzY42oW1ij6mfKinvOL9kGcNf4/s8r8Mp7sIbdbwO7Z31eccxH5/8GPum6v1Xkdf/9nex5jsoc82xVxTyvfQh5r8FmJJ+zYF16jHMAH8AGbzgH+Ggd2rE6xfOwNhenYvV0k9wTd7lnPpHxy3zAKVgnnRewBoPHla07E7f3YNeTd7FzX97ra7qut/DB9jLaa4l5TF6Xz6v3ubwur09PXi871S5ASUlp+k75i3VuXXa68PTisRHe8zp3oUwvqOnF8qyatW8JTMjmw3oPtYBzOmyzCtbo+96CdSvglUZV6R4gzxxY44oLC76Hsbm8Q755KEN7Uf7cjdhiWI+yx5i6B9dEbEquAWNRsvbFXUO+p1/qp93cTzcPdIxlJnK92t0bP3ddhTdHtKeK/Hlu+Uy9jnk32jvkWcy1njKE73BUL3QNV3vGF1OdFzPLV8c6MDyQ+w0sgI0MP7FK3RldqwKrYZ0Qpmlwht2Et4Aryo75IN9vo73ejfYOeWrzerfam+L1oepuotcHOa5Ge70brxTk0Tm9RO1N8zqD3DeTec7w/9+DzYrzMvCRDtt82LV/P7e8Z3HvVneHPO9znQfnfVSyH7rWnvFFvrFC6qe0YcMdue1WwDrE9uqcPmTtNOi5lEFGJGvyOb1b7R3y1HJeH452GnBe70Y3zTunrwgsNNSYN8Xr3erukKcun3etvQk+71Z7k7yOTYt72VBj3hSfD0d7hzx1eb1r7U3weje6m+TzIR5bY73erfYOefRcWpLuJnp9kO+30V7vRnuHPHWd16OsZ+xGe9O8PpSyaD8nzw08iDXm2rNoe2BdbFarW3LLlwS+iDXAn3WkurvQ3jEP1mH7CaxDRcff30DfbVXaM75ZDJi5IO+a2LvSPwCzZJZviI2YekQv4j4M3dtjo4mmnV1GZ/PQbmR3We44K6kL66Tdf5tPYKP/b1GkCdjFtV+ZW97TmHehfaBz0FzYqLo3+Dmy8HvMnYsq+w6K9ovV9U4TP2AHbPT2/DlmL+A77qnZqvSL/32w7zvtVDE693kGmTYmRV6vOOZRel0+r97nWb/4343x+lDKaaLXh6i7kV7vVntsXi8j1S5ASUlp+ktYr98NgLXIvGjJnJRnBG72i942vmzABz3aPW/SacX2L0n7Slhv8o2BhTPLszcj6XTbx+aO6z1Yj+0WsGG6jnbv+gnA69jozD2tbB6O7gHKShu07JVZNoeX/xH8JqyJ2jP50xvDCdgoFn8G5m6CX4ZQZur19Hs4twTdk4aQ5ybf/+655du4z58FVvNlYzI+X9C3+zYlND4fifaCfAeTmUrHl82BTQPU8ykJe6w9Pe+kXp/ft/tlCb/RrnUz9HP6kb7dCb2Ot5e/OFYBvhQdHqQa7PVhay/IV7XXe6m9Sq93rbtBXl8O+CCwGQXTaA4U8zq9PhLdBWVV7fNeaq/M58PV3iCvrwf8HjiQ4unlpnnO8OXjgI/TnvpuuVR3xuur+Xafy8ejLt0dyjrR862a8/pewPqkFr48AAAgAElEQVRZLzVJO5kX0ZmYr+zbfd+/i55WlA9HexdeL+25FGtQ/hA2xfeiHfI07pw+Uu0F+ao+r/dSe5X3L13r7sLnZZ/T13dtTwIXAPMPNeZ1en0kugvyVe3zXmqv+v6la+1N8Dr2cu+PXv7fin6nTfT5SLU3wOu91F7lOb1r3U3wuZe/CvZC9QjsZfd82bg13OvD1t4Ar/dSe5Ve71p3g7y+NLA2sAyZhpG5PE31+rC11+n1Huuu+v6la+0N8vpMuf/zDZvWxp5DUi+P8pTOlPZbYJ403rQbTc2NNTR6pGAfM9SlvUM5y/qxfCG3fE6G8M6kZu2jsXqY1OuzA5OxTgzz5/KNq0F36uMJFDdCT9evgw1CdgsF9TpVJNd+M1PPujwr8Hn3x1XA7On3kYn5YtgsdL8iU+fVq5gPR/sAflnHj+Wo3PK5aM942HGU+Jq1p17PXkv/A/ydTEM/rA6wig5ped2pl2emuMFiun4b/w6+S64zTw+15X+XRb/Txnm9W91N8nkPtVfu82Fob5LXB/Rdg73ele6Geb1X2ht1Tq8i1S5ASUlp+klYBchFWKXUq36x+BPWg2aqXla0e2F9qENZab5s49iJWC/il4H391j7vNj02m94agF/AY7NXKjTz72x6SoOLDiu//NtH2HqhhYTaPco7uV01iPSnSsrrVS5yL+/hf3CuRE2/Vxa9rxN054/Bv97JuArXu7hTfLLELw+I3C9l/vBHuu+BqtQWye7/wIfHEZBQxWsUdSZtCvm5sqsGw981tftWULMR6Q9G3NP1wPPYVPjjM15/c/07sGnZ9o7eH0i8HXfbr+mxrxA93jgdmyapQ177Jf5gUux69F/Pd0ErJTJM2Yg7TV6fcTaa/R6z7RX7PWexrwGr38PG+Emvff6B/ZiZ/RQtNfh9V7ortnnPdFepc/LiHuVXvfyl8emUmthoyRNMwWx5yt8zgAWwaabbQE/zq2bEfiar9u2SboLdN6JjRox2v/fMOP1B5qqvcAvE2h3fty5aX4ZxOulPJdio8H9yPXcB3wUr0DOx7DTb5T67l9GrD0bc6o9r/dMewevl3X/0tOYF+gu8/5l5kxM7sNe5GzedK/3QneNPu+Z9ip9Xkbcq/J67jf6KHZNehJv3NRUn/dKe41e75n2Kr3e65hX5XMve17gCuz54jXX1gJ+hjfOo4HPpL3SXqPXe6a9Yq/3NOYVe30ScCXWqCCtO7oZG9wofZ4eO5D2Gr0+Yu11eL2Xuqv0eRkxr9jr82P1Iz/23+uxFAyYRLsO5Yrc8nmBn/q6b/iybIeNJbGRvC9ngHd9dWgvyLef50s70I/DOhp+H6tn6FlHgF5rz3rH/14Waxx9Y2S60/fqZ/TSK172JKwjynz5/ebyXeEavpZbvipwj6/7jC8bk1m/VvZ30CTtBfk+5fmW9f9Tr19ObnTUpmkv8MzaqdfoYUeACnSng0eU0dF4PuDTwGnYYCFbdqO9Lq+PVHdBvip93lPtBX4pxecVaS/b66cClwA/AL5EQSeshnp92LoL8lXt9Z5pr9LrTUm1C1BSUpo+Elbx8BJW4fwdbJSFi7DKiruB5XP5x9NhFKkO5a+GNaJt4aPn9VD7YsDvgH/6jcReWOXaU76/Mwu2mWZEoMy6y7FKiWeAzwC7+o3Pv7GRARdrqO60cuivwG3Y1O4ne3nvAp9vaswL8r4Pm+bkFawyYcGItK/mv6EW8C16NzrB1tiLoRbwpt9gTch+9wV/L9yhrIA1KEpfqh6C9aw8FRtl4ZdkXjw1SXtm/czYS7JrgRWAk0ryes+1F/jl69jLkCuBOSLS/X2GeAPfpfYDsPPtM/79noONAtHCRnRY3fONGkx7DV7vmfYavN5z7RV5vQrdZXn9UOzlUDpa4UexnuRPY72WN2yi13upuwaf91x7FT6vUHspXs/sYyUv/w7//AwFIwAwwHMG1mnxYd/+OuBDwAfc6y8CP6GcWWlGpDuTZyH3x4XYi9Cs109rYsw7lLsqdp/7BvbM2NNZjErWXspzKdaA413/TX6GTMeiXL4m3qv3THtmfVXn9Z5rL/BLGfcvVegu7ZyOdYZ/DXtmXy23bpqRWhrk9Z7ozqyvxOdlaC/wSyn3LxVp77nXgS/49/gU9hJ0GazhVYvMNL5D+Y3W4POeaa/a62Vor8LrFenuqc9p1yGvizXefAJ7ebs9sEXGs3t5vsY8k5ahvSqvl6m9TK9XrLssr2+JdYh+FnsWOxIbwW8K8AJwmOcbM5j2GrzeM+1VeL1M3WX6vAbtZdY1vuZenEx7QKNbgU09T9oBYwasXmnFgnKWx94Nt4Dj8Pdz2Cj9V2AzGm/SRO25Mq/HZs6Y273+Gff628A5TdVO7h4Za8h1F/YOf4MYdGPnys2xZ96HyMwK3iPth9N+97XDIHmXBr4ILJNbPgZ7j5bO4L0X7Xdoq2D1ji+Re4ZpgvZcntHYdel+bPCIldzr/3Cvn5d+Jw3Unvf6xtggDM8C721wzPO6P4hdH34LzNljv5zkv803aXema2HXptmy322TvN4L3TX6vNfaK/F5RdrL9PrJ2H3dc0w9AOnlwBIN9vqIddfo9V5rr8zrTUq1C1BSUurvhFXgnI41hvoR9pA1k6+bC+uV8zbtRlFDukBgD2wTsOkhTvMTdgs4iw7TlI3gGI7xso8h86LfL87P+7qPMUhjA6aesu3jmW1bWI/5q+nti5ae6M6VuTxW+fYHrAF6y7/XBZoY88x2o7CGLVtiDfIe8DIupvc3hb3WHrCG4ptgIwXe72VcQGYakRHoHY01WHosU+4jWAX6FsMpzz+Xxhq1v+7lvuO/9aso6InfBO25stfzMn9Ju9dlz7xelnb3+sLulzMzfvk2val8Lkt3wCo/N8Be3KS6z6NgGqYRaN8P63Dxc+x6NN7XLYe9aHiLIY68UoPXe6a9Bq/3XHtFXi9DdxVeH4+97HsKe7mQvfcaR7uh1zZN8nqvdVfs81K0l+3zkrWX7vWCfW6Mvcw5Grs2PUUXoyTTrkBaFZuJInuf3sJe5M7VNN25snZ0rT/AKj9LuVfvtXb3+hzuly8z9f3u7L3W3WPtpT6X+u8oHaXwIt/PsEe1o9r7l55qz5Vd9nm9FO2Uf/9Slu7KzunAe7AOddcDMw4WzwHWVeb1XurO5SvV52VpL9vnJWsv1evY7Bkvux8v9P1M9HUn+76G/HxRpc97rb1Kr5elvWyvl6i7ynP6RdhL/73IdIzEnjlawAGppqZ4vdfaq/R6WdrL9nqJuivxOu1RqV8D9gBm9uUT/P/0uXKNIZRV9f1Lz7RX6fUydFfo8zK0V+X11bH3WzcDm3rMVgLO9f09gw9exMD36enMEh/COnK0sOfxu7BO9u+6/6fpdF239lyZ82GNk36LNV6+t9deL0t7puyVsAHY/uTH8n/0bhCpMnWviDWifRhrPHeQl9+LBmgL0R4l9gWsTvAauujsX1DmQdj5/B3s3fSNHvN3sHqkXsW859q93KVd68/9WO7rtdfL0p7zzGFYB4CXsQaoY3pQbtm6lwc+gQ2w9TywL7nOnCMoe0nsHdfz2GxXH8beex2BXaOeJjcDVhO8XobuCn1eivayfV6R9jK9/l5s1p8XseeNbbH3vythAz++TofRxmv2es91V+j1UrRX4fUmptoFKCkp9XfCGm7f5RezRQvWfw+rkOqq9ww2jc0NfpF5EZvKav0S9Aes1/DTtBu4BNrT/O3vF4tHgfW6LHtFbOS/3ekwclbTdNNusNzym5SNYok5dpPZwnpr/bLb76tm7Ze79uew0Xh6qh2r4HsF2Nj/PxyrPPsuMG96HMMsez1gF+Dgbn/ndWrHbrpTr/+JHk9TWLL2a133P92PjfcL1nDwB7QrP+6gx+d0YHHgj1hl8ZKZ5WlF8sd9/2cO8xhK83qZ2sv2esnaS/N6Wbor8nrAHsjvoGD2D6yDUIthXsPL8nqZuivweZnayz6nl6K9Cq9nj8E/d8AaAcyGjRrRAr7JMF9iYpVNH8VeavV01JyydAPfyHj9oV57vSztwOzYKOjp/W40fqGC51LaU1N/KrNsZqzRwfuxhgeLDrPssu/VS9Fe9nm9ZO1ln9d7rptqz+kH+H628v9nw+pNjsBG7TsRH9Wty3LL9nrPdVfh8xK1l+rzsrSX7XVgb+yF1q7kGoi51hZwtP/fVeMW36bMZ9LStJft9ZK1l/lMWorusn2e2c8HfB9XFqzbx2PWVUPRzPZln9NL0V6210vWXvb9S891V+j1tGPtJZllwdP4TOxuy/+Wh1B22V4vRXvZXi9Rd+n3L2Vor9Dr5/s+1sosS+tJr/J1lzPIQERMPbPEsti7ht9gjaJvKCnuPdGeK3N92jMyp3UwGzRdO9b4eX/3yZ+x0Vb/AKzTcN0zYB0ffo69m57iutfqse60fuhX2GwRV3iMPgqM7bKsrNc3xBr7Poo1Rr+5117vpfZcuTt5uY+553vu9TK0Y+fUPbD2KX90z9wPrN1w3TN5zH+INbZ8270+rPvmDvuYgA2A9zZ2zZ4vt/5MP64T/P8BnzWq8nqvdVfp87K0V+TzsrRX4fWZsNlL0o5L8+bWH+/aPzzE8qryek91V+z1UrRX4fWmptoFKCkp9XfCet0sV7B8HLAz1nvrEuwl48TM+sFuEEdjU/B9BX9502Pd6cPleGwa+heBRXzZ/3qGYdNSXOAXn3MZQkULw2wcW6fuTLkr+Xc2rNF3atKejnCxIPbCr6eVExVpXwx7ONy4x7rH+uccwJqZ5SsAtwD/wae27DYeZfq8ZO1pA/wPYg2Xy/B62dqXw3olbhCJ7vT3syb2QLhZSZ5ZwMtfMbMsZPafjiJzRrpuKNrL9nqJ2kv3egXaS/F6mX7xz9K8Tvu6MU2Pauzea3usweRPsVF85sxv20l7mV4vUXcV5/SytZfp89L84p9len2aZwWsk9HTwKwet7uwRrvbMMjondlyS/Z6WbrT7/JQbJSi0u7Ve609U9YGwKfp8RTLZWunxOdS2tMQL4Rdcx4ElgKWwSrMH6bdWOJt7HkhnbqwtnN6ydqrOK+Xrb2se/XS/OKfZZ7TQyZ93jUu7es+i43S805GfwubUWXAkW/K9nqJuqvwednay7x/Kc0vFXh9ArnZ4jIx29q1/nCg32TVPi9Ze1XPpGVqL9PrpfjFP8v0earxfa7xenxkYT+mTbAXx49jo7RuSXuAgAFHdi3b6yVqr+K8Xrb2su5fSvNLhV7/sGv/MjYle/Y6NRr4Dnbv1QIOapjXe629VK9XoLvMc3ppfinb617+RKzB1Qv4bFquN/v+6iHXvecQypvG48CkmLTTHln938DHYtCeKXdPYDLWiWDXiHQfgr2DuhHYvaSYb401Nh/n/++CdfS4G1h5GOWNyv7tadFItKdePzLj9YNi0J7x3P9hMwH8BNgtEt0TsPP5K1hj8SH/RrrYx3JYY8jTcsvTd8Ab+3d+CUO8J6nC6yXprsTnZWj37arweVnaq/D6DNg7gP07rL/av/NFuiizCq+Xobsqr/dcu29XutebmmoXoKSk1D8JWBtYgw4j2dF+YFseOBb4h180fgv8F3vIOyyTP9vbaSlgj1x5XY9aM4D2nbCp/bYDxufWXYVNA7F90f6BdbHeTP+iYMQEbEqSwylhqvkqdWe+v57EvWLtPa0IjVX7QLpz+UZjlVKvYdOjLDOYFmxUhYM7rOvF9DiVaad9Y1u610vQXsl5sayYl6U9850uOMA2h2HXpI8PUnalXi9Te9leL1l7aV6vIuZlac8sT6/Z6UujFbDGkn933b/HRo14Evhykb4yvV6l7rJ9XrL2nvm8rrhXoD3b2eIIrCFXehwHY410b8rkWZVcwxcKnjMq8HopurEGykNu2NMk7TH7pVe/1U66fV062t2V2MuhFvbc8RXgUqwDRgu4rEPZtd2r91o7Fd6rl6C9qjqMUmJekfaTXNtewNH+9zexWVTWwK5PLex5eoe8tjK9XqXuin3ea+2V3L+UGfeydRftC7v/eg4baXPMQHEs0+dVa6/S6yVor6z+pYyYl60da7B1i/8GL8RmqjwTeIL2+4C3Mn/PO5j2qrxehvaqvF6S9tK9XmbMK9C+j+u6AWucMiq33R1Y44MW8NcOZdfl9Z5r76XXK9ZdVf1LaTHvsf6ijtG3YY1018ktT7/zg1z3b/CGvAVlzJXXXELsy9ae1hdM8O2GPQJyXdr970V7Ffuq/II1nFuhl57poH2WzD7nwAboamHPHjPnPdyh3Nnz+ehRfV3V2rEGnYdV4PUytM+A1eOV6fWe6c78PxuwSplexwZeTH9j+brPtAPpoCMvl+31qnRX4fMStffU51Voz/xfhden+U79+05nqL0BOAGbnXnRoca9KBYx6K7I62Vp77nXY0i1C1BSUoo/YS9G7scaZr+BTdVwHt4LMX9xA77kJ+wbga2Azfyk/bQv383zpg/HMwG/83W79Fj7VlgD2ym0Kwbvod0LfqxfVFrYi9GJHcpJpzo/Pj3OzLqrfd0p07tuaW+mX3J50xujBYDv+TafZJAbJGx0wxZwQJUxl/bea49V9yDaC1+M+DZpY8ZzfZtpZpeQ9v7UHqvuQbQX9qym3eDlRmxa4zWwkZPSUVEOzR5fDTFvtG5pj0M7NhvKA7RHq52EjZbSwu69nsemUF46s00pzxmx6pb25voFa5D+H193O7nOocDmtBu97OLLsi9sa/uNSnv119Im6u5C+/a+/lzgEeDSgnLSOqWryE3XXWPMG6db2pvrlw7bLYvVqT7NAJ2q6465tMsvQ9B+sK8fjT1HPOjr0pFnb8Y6zk3y47jJl59HbrYUae8f7bHqHkT7Ib5+HuCvvvxQ2o0PFsVmkHgBm5Xods/zwQb8ThutPVbdfaB9S6w+KK37zL7XHQd8HZsNZc/cdun7gfHAna5tB1+WrTc6GBuNc33/v5cNuKrW3stGXFFqj1X3YNo7aN0AqxP9G7DRIGWPdu0PA6tX6fUytPcyxRr3WHV30p7RWdRAPc13hP8292lKzMvU3csUa8z7UXuHfAHrcPeAa74XG2H8cax920MZfaPL1l617rK9HkPMY0y1C1BSUoo3YRUQ38QqKH6NjaJwOjZlQgv4PsU9r98HbF1Q3ra+3S1MWyl3CvAM8L4e6t8Fe9F5t99w7Ax81TW08IdNYCOsMuVxYJVcGWnD87V9m7tpTzeSXnh28ovOetOzbmlvrF92w18AMe3IP5thL4h+D6zly8bk8qSjG34EeBFYt8KYS3uPtceqeyTasREeRmOjQvwVq3QcW3B8o6W9f7THqnsY2lMdk4CtCspKr0ePAxMaFPPG6Jb2OLR7/kuAP5AZCQAbdeBNrIJoMjaK5yy5/fT0OSNW3dLeaL+kM/jsAfyS9pT0o5i6IW5aif4d2vdcdf9Gpb36a2njdA9R+x5YRf/KWOPctBHMFqm2jL5lsJnf3gAW8mV1PR81Ure0N9Yvu9PhedqX3Q28DKzRofw6f6PSLr90+xtNnxcWxGYl/Bz2rmBcTt97sYFi3sRny6JdVyrtfaA9Vt1D1L6X59vLdb3leS/CRql9E7gOuy6l9157N+R32kjtseqOWTswP3CF7++fwDa+PF/XmY6sfAP+2yzQtrfnua5gP6f7uot7GHNpr1h7rLq70Z7Jnx0Z9ASskfqF+GwRdGhghtU3tcjMdijt8WmPVfdwtBdsfy3WqWKJQfLVGvOm6Jb2uLRjdaf/BLb1/0dhs2+c7OX8uGztseqOXXusqXYBSkpKcSZgTuB8rPLgDDIjVQKbYL3Pn8V70Q5QTvrwNhZrJP401tN8VqZ+4Timx/rHYi84/w2snVt3KPAqNuX81r7sIr9wfA2YI5d/DDa9zpN4g3RK6i0Uq25pb7RfngC2z61LHz5nA77ox3ImPvI49lC6iP/d0ynDpL0+7bHqHon2TJ7lPc+lueWjaI+Y0qjfqbRPf7qHqz2vhfa9Vzo67Z+wRroLlaE5Zt3SHp32O4Fr/O/ZsdHbWsDrtBsupi/8s501evacEatuaW+8X3bMLF9hgPK2c+2X+v91Px9Ju3R3o/3v+EiEwFnYC6EWsH9WH+3GuD/y9T1riNMvuqW90X4Z6BljIvZi7A0KZj5sQMylXbq70T4ZH3XTly/hy0/2///3PsA/r/ff6DSDwEh73Npj1d2F9idpvw/YExt57nWsYe/jwJGZbT5O5lol7f2jO2btwPuBn/q+/ow1QryazHT3tOv+58IGI2oBO+fKSfPMgTXauRV/L8bU73n3lPZ4tceqe6jaO2yXal0R+BXWJuJDFNQNZfIuTKZDhrTHpz1W3SPRntl+Nuw55Hb/f5p3uk2Ked26pT0+7dnfYzYP1n7n79izyfK5bWr3et26Y9cec6pdgJKSUpwJ2AIbwezc/AUa61mT9p7ZzJcNeIPrf6/o29xdgf5JWE/4y1IdtCsGxwKf9/U/B+YDVvELyqvAvrRHiUhfEC2KVaTfJd3S3hTtXej+KX6zRO63it2g3Y/dVG0JrIQ1Vv8VsFgmX09fHkl79dpj1T1c7bnt05EjdsksWxI4EjgbmCTt/aM9Vt290J7XBCyCXav+wrSzpDQm5nXplvZotK/gy28FLvPf6KtYpdKlwFFYJdPT2GjjpXQwilm3tMfjl4IyAu3Gi7th16dvFeWT9ri1x6q7S+0/x0Z8WQGbFaWFjfgzm+dNn6dnxBrBvAHM34CYN0q3tDfeLwM9T1/ox3HIIPuq/Z5R2qdP3cPQnt53bYm9Rzgw1ZP5HA/c58eynLT3l/ZYdXep/SZgaV8+J7AQsA7Tjkz7Sdc9zYw/0h637li1YyOCX+X7ORtYzPW9Dnw0lzd9hjjY8/8RH8QlLcs/FwCeB35XtH0P4y3tFWuPVXe32gcp5wCs/ugG/LkCm5n8Q3g9aa9+n9Jen/ZYdY9UO+17rXWBKcBpufWLA6vT44E6YtYt7XFqz5SR1hmNwu7bZsM62T2BD1on3f2hPfZUuwAlJaU4k1+MjwJm8v9H5T7P9JP6Dh22/1+P3Ux5N2I3uNtUoH8913dTbnmqfzmsMvEt4AhfdjjWa34ycFBmm/mwkYFeB/aQbmlvivYudL+JTek3Jp/H/z7Qj+1e4DEv8xfAfNLeP9pj1T0S7bQr16/ARlKZFZs1YnfX3MJGAJpL2vtHe6y6R6Ld1+XvvRbFRi38L7B7WZpj1i3tcWnHOhW1sMa5dwH70x4l4FO+7jpgZumW9iZoH+5vNP195n6jS2P3Xv8B1iwz3tJej/ZYdXepPfs8vS9WqT8FOD6zzSTgROBt4IvSLe1N0T7c32guT9rZ4jh6/IJf2pulPVbdw9Q+Cvgg1kj3B8BSmW0mAaf5urOlvf+0x6p7mNrHDlDWcsCjwEPArNLeX7pj1g5sxdTvrnbE7qfuAJZMj4FMBwvgZ36sF6R5Mtuvjt13Xez/l9lJWtor1h6r7m60d9g2PZ5FsMEApgCfwe7BHgOeAjaS9v7RHqvukWinfb06wX+zG/n/8wC7YjMe3gOsIt3SHrP2XBnZutKNseeMH2Ed8mq9ljZNd+zaY061C1BSUoo3AbMMsO4av4gvOkgZMwPbYKPpvAl8FZv+utTKaN/vv4G/ASv6svyIJ/sCLwG3+03IrFhD3bf92L4FfAnrlTQF+CGwgHRLe1O0d6n7V0W/V2AccAzt6YwnAzs1LObSPh3rHql2YBZs1Nn7sFkoLsUaCDwFfEja+097rLpHqj13DNvQvh5dAMwj3dIesfbbgAWx6YsfBE4i8/Lf8y4HXE7JnUdj1S3tUfil0280fZ7+CfbccSp2P9ak52lpn451D0P77cC82Axwu2P1RC3s+flCrFHAFM+3rHRLe1O09+g3ujuZEfTL/m1Ke33aY9U9DO23AXNjI9He63rvxF70H4l1mH4Hm0GlcOYgaY9be6y6h6G90+90Jmzk8Z8CLwC7lq07Zu2x6u4D7TNm/p4V+K7//k7K5UtHV14D+DX2PHEdsBQwF7A51qjnX5TYYFHa69Ueq+5utBdslx3QaFfXnD53PEU177+kvWLtseoeiXbPfwfwMDYr1gbARa7/n2RmrpVuaY9ZO5nGw8BEYBfsHu5vwFrS3Z/aY021C1BSUuq/hE2Ddy/wJ/9/VG79TNj0qJ8CrsQqO14Hjq5Q4wzYi/rXgI8wda+gtBflgsDNWGXhmpn1e/lNSgtruPg0cIJ0S3vTtA9D9xq+LK1wWcu3n4I1WvxUg2Mu7dOp7pFo9+UbueYnsMa6bzOEh1Vpj1d7rLpHoh1rmLs8cArWke45bAr6pp9fatUt7VFqXzlXTk+nbO1X3dIenV9mAZYFPk179oj/AkdKe/9qj1X3MLVnn6d3wBrovuvaHyczErN0S3tTtI/gN5odzXAZrO7od8C4Bsdc2qdT3cPUvpYv2xVrjNvy32gLeBE4Udr7V3usuoepPf2djsHej52OPU//E5ud9hBp70/dsWsvOJY1sEaIjwLr+LL8O941gZsyv9GngOdd+0elffrRHqvuoWrP5B0NbIi1aWhh77+OlfbpR3usurvRDiwJvAz8FhtZ/HnsXdhJ0i3t/aQ9XY4N3HUO9v7rGSpoiN5PumPXHkuqXYCSklL/JNqVEyv7Rfvr/v+YXL7x2MvEV7GpZs4D5qpB775Yb7EfA0t0yHOK33Cflls+FpuG/n0MMGK5dEt73dq71P253PJjfdsrgDkbHnNpn451j0Q78Alf1gIuA+aW9v7XHqvu4WrHRuE8HfgP8Ahwdgznlybolva4tGeWV96wOHbd0h6Pbv+NfgPrbDEZ+DrNf56W9ulY9/+3d99hkhR0HsbfLyBiQPA4VBQEQVB8Hj0MKGIAQRDDyZ1gxlMQTs5wIncnZhbTGU7FjJFgzmACRREQUFF0RX1QFFxAQTAryC4Cv/ujarRpemZ7wk517byf53mKEEoAABQASURBVKmnprurut7q2VmGnd9Uz7V96LFNaa6iv6Hdtk9q+wJ0b0nzw9Befd9l+9LqnkP7/7a31wE2Bp4NPBM4ENjY9rW/va/dc2gf/n+MbwE/At5Gz7736rK9r919bx9q2WCg8yhg/fb+9bjhsPqGwJNprtD4EZp3qbV9ibX3tXt17UPbBTgIuKzd9jg6+P7L9m7b+9o9Tjvtv4sCj+DvVxW/HvjEpP79Msndtk9ue/vxzWkuPLqCZhj5SuADk/73yyR29729L0vnAS4uLmvfAjy9/Yt7n6H7b0U70ArcHdgD2LLDzg1p3tZvJc0/EG7Q3p+Bb0x2YWBIl0V6K8u1sdv2XnVP3b81sL3tS6e9r91zbW/vexjNPybe2/al097X7nm2bwHsDGxht+1razv9/d6r827b+9Pd3rc98CjgTrYvnfa+ds+1va9fo5PQbbvdtk9+e1+759G+Xhettnff3tfuebRPDTJsBtze9qXR3ff2EeeyLXAuzVUU9x167Eb/LZo6j0lYbLd7TbTTvIPESQy8o2fXi+12L3Q7cGj736gzgft23dznbtsntn1qIP0AmqHi1wL36Lq5z919b+/Dsg6StPB2pXkLsS8BJFk/yS7Aq4GXAVTVD6rq5Kq6qKvIqvoz8Hqatx4+GNizfWjdqrq2/fgu7frKdp9a1MgR+toNtndhjt3XtusLq+q8Rcy9AdsXX1+72+PPur3d70tVtX9VnbNosUNsX3x97W4b5tp+SVWdVVWXLFrsgL52tw22d2CJfe/VeTfY3oV5fI2eV1Wfr6qfL1rsENsXX1+724Yl8zU6Cd1gexf62g22d6Gv3TC/fzvqmu2Lr6/dMOf2a9r1ZVV16SLm3kBf2/va3R6/t+0jXEj7rm3AfkluBpDkSTRDOSTJ1MZT5zEhbF98fe2GMdoBquqjVbVXVX2rm8yRbF98fe2GmdsPard5H/DQqnpAVZ3dTeaN9LUbbO/KTO0Httt8AHh2VR1WVed2k3kjfe2GfrdPvpqAyXIXF5e1ZwFuB/wc+Gx7+57AS4FLaH5b60Xt/ZNyZZF1aX4j6K/A+cDOA4/dC/gGcAGwedeta0O37XbbPvntfe223fal0t3n9r522277Uum23W7bJ7+9r919bu9rt+122z757X3ttt32pdJtu91LqX3EudwWOAG4Bngj8C7gL8Dvgdt13Wf7ZC197bbd9qXSPUb7xLxbxNrSbfvEtk/s12lfu/vePulL5wEuLi5rx8Lf32pjD5rh7XcB+wPfbm9/Drhj153TtG/U/sfleuBS4IPAe4BzaP7x5QXAekzIIHrfu2232/bJb+9rt+22L5XuPrf3tdt225dKt+122z757X3t7nN7X7ttt9v2yW/va7ftti+VbtvtXkrtbX8GPj6QZiDn+nb5DBP6c17b7bbddrvXrva+dttu+1Lp7nt7X5bOA1xcXNauBTi8/Uv6HGAVcB6we9ddY7Y/HzgXuBq4gua35nftumtt7bbdbtsnv72v3bbbvlS6+9ze127bbV8q3bbbbfvkt/e1u8/tfe223W7bJ7+9r922275Uum23e4m1bwo8E/gOzc97vwvs0nWX7ZO59LXbdtuXSnef2/vabbvtS6W77+19WKaurCtJ85ZkPZrfOH8qzVspLKuqt3ZbNTtJNgQ2oHkbiB903TOuvnaD7V3oazfY3oW+doPtXelre1+7ob/tfe0G27vS1/a+doPtXehrN9jehb52Q3/b+9oNtnehr91gexf62g22d6Wv7X3tBtu70Ndu6Gd7kvWB/wFeAfwReEFVvavbqvHYvvj62g22d6Wv7X3thv6297UbbO9KX9v72g39bu8Lh7olLagkjwW2A/6vqlZ13SNJkiRJkiRJkiRJmln7c957AK+qqpVd98yG7Yuvr91ge1f62t7Xbuhve1+7wfau9LW9r93Q7/Y+cKhb0oJKkvIvFkmSJEmSJEmSJEnqjT7/nNf2xdfXbrC9K31t72s39Le9r91ge1f62t7Xbuh3ex841C1JkiRJkiRJkiRJkiRJkiRJHVqn6wBJkiRJkiRJkiRJkiRJkiRJWsoc6pYkSZIkSZIkSZIkSZIkSZKkDjnULUmSJEmSJEmSJEmSJEmSJEkdcqhbkiRJkiRJkiRJkiRJkiRJkjrkULckSZIkSZIkSZIkSZIkSZIkdcihbkmSJEmSJEmSJEmSJEmSJEnqkEPdkiRJkiRJkiRJkiRJkiRJktQhh7olSZIkSZIkSZIkSZIkSZIkqUMOdUuSJEmSJEmSJEmSJEmSJElShxzqliRJkiRJkiRJkiRJkiRJkqQOOdQtSZIkSZIkSdICSHJqkuq6Q5IkSZIkSZLUPw51S5IkSZIkSZI0IEnNcnla1819k2SHJMuSnJnksiTXJPllko8kudcM+62b5JAk5ya5Osnvknwxyc4jtr1Jkn9N8r4kP0zypyR/SfKDJC9PsuEMx9k8yfuTXJpkVZIVSY5Mcus5nOseSd6Q5KttbyU5Y4bt75DkOUlObI+7Kslvk5yc5DGzPf7A894tyceTXJFkZZKfJDkiyc1GbHuTJM9NcnSS5e3np5IcOIfjPq3d95gZttm13ebU9vayWX4NrhjxnDu1n8Pzk1zZvo4XJflEkn2T+DMySZIkSZIkTZT1ug6QJEmSJEmSJGnCHDHivkOAjYA3A38Yemx5u/434OZrsGttchRwP+Ac4NPAlcAOwBOAfZM8rqo+M7hDkgAfBfYFfgK8DfgH4PHA6Un2qaoTBnbZpn3uq4CvAV8Abgk8DHgp8PgkD6iq3wwdZxvgLOA2wAnAj4H7As8F9mr3+e0szvVZwN7ASuBnwOoGw58DHAb8vO3+FbAl8BjgoUneVFWHzuL4JLkfcApwE+CTwCXAbsDLgN2T7F5VqwZ2uQVwZPvx5W3DFrM55jydOuK+HWhex+8Dxw899revySTr0/zZOAi4rn2uzwOraM5hN5o/Qx+j+fMmSZIkSZIkTQSHuiVJkiRJkiRJGlBVy4bva6/GvRFwZFWtmGa/i9do2NrlQ8B+VfWzwTuTPBn4IPCeJF+oqmsGHn4CzTDuWcDuVbWy3eco4Ix2n1Oq6s/t9n+mGag+tqquGjjG+jTD3o8EDqcZoh70DpqB7v+sqrcO7PdG4HnAq4CDZ3GurwVeTDMcvgXNsPZMzgZ2rarTBu9Msj3wTeB5ST5UVeeMc/Ak6wJH0/zCwd5V9dn2/nWAjwP70JzXawZ2+wvwCGB5VV2WZBnNa7UoqupUhga726/BvdumZTPsfhSwP80vWzyuqn469DzrAvsBD1+wYEmSJEmSJGkB+NZykiRJkiRJkiQtgCSnJqmh+3ZNUkmWJblPkpOS/DHJ75N8KskW7XZbJ/lokl8nuTrJ15L80zTHuXmSFyZZnuSqJFcm+UaSJ86h+d5txxVJViW5KMk7kmw2Yttj2nPZKskzkvwgycoklyd5d5KNxj1uVb11eKC7vf9DwE+BTYC7Dz38H+36JVMD3e0+36a56vKmNEPfU/f/sqreMTjQ3d5/DfDq9uauQ+e4NbAnsAJ4+9DxD6e56vdTktxi9Wf5t+N9o6p+VFXXjbn9p4cHutv7z6M5zxt1r8YuwPbA6VMD3e3zXQ88v715cHsl9KnHrqmqE6vqslkcp3NJHkwz0P0bYK/hgW6Aqrquqo4FnrrYfZIkSZIkSdJMHOqWJEmSJEmSJGnN2xH4evvxe2iuxvwY4KtJ7tre3hw4DvgCzSDuyUluOfgkSTamuSr1q4HrgPcDx9IMNH84ySvHDUryKJqrXv8z8BXgjcBPaIanv5Nkq2l2fV27fJ9m8PmXwEHAZ8Y99mr8tV1fO9B6U2BnmitIf33EPie2693meoyh/b/cDj3/TXsF8DNprni905jHWWjTdc9k6pxOGn6gqi4Ezge2BLaeX9pEeEa7PqqqLp9pw6patQg9kiRJkiRJ0tjW6zpAkiRJkiRJkqQl4BHAfu2VqAFI8j7gAJrB6jdU1asGHnsp8HLg6cCbB57nSOCewGFV9bqB7TcAjgdelOSTVbV8pph2WPwYmp8T7FpVXx947DDgNcC7aa5aPWwn4O5VdXG7/XrAKcBDkty3qs5ezWsxU9f9gLvRDIr/cOChOwPrAhdW1aiB5qkrMm835qEOaNfDg853adfnT7PfT2lek+2Ar455rAWR5FbAPkABX57FruOc03btcsGcAyfDA9v1on5uJEmSJEmSpIXglbolSZIkSZIkSVrzzhgc6G4d267/SDNEPei4dr3D1B1JNgH2A74zONANUFUrgcOAAE8ao2dvYBPgY4MD3a03ACuAPZLcccS+L58a6G6PfS1wdHvzvmMce6QktwY+0N48tKquG3h4o3b9x2l2n7p/4zGO82iaKzr/guaK44MW7DgLKUmA9wK3Bd5ZVefNYveJPKc1ZLN2/YtOKyRJkiRJkqQ58ErdkiRJkiRJkiSted8Zcd+l7Xr50AAzNFeqBth84L4daa5WXUmWjXi+m7Tr7cfouVe7PmX4gaq6NsnpwFY0VwW/eGiTUedySbu+9RjHvpEktwA+C2wLvK6qPj7bp2jXtZrj7Ax8GLgK2Keqfj+f4yTZGDhkxHZHVtUfZvncM3kD8Fjg68ChNwhKdgD+ZWj7P1TVkWM+91ivXc+sTeciSZIkSZKkJcKhbkmSJEmSJEmS1rxRV0m+drrH2sFq+PugNjRX1oZmuHvHGY51yzF6pq7efNk0j0/dP+rqzaOGlafOZd0xjn0D7UD3F4AHAm+sqsNGbDb1Gm004jGAWw1tN+o49wdOBK4HHl5VZy/AcTYGDh+x3TGMfp1mLcnrgecBpwOPrKpVQ5vsMKLhImBqqHver908Xd+uZ3r32KnHrp9hm3FcBtyR5pchLpjnc0mSJEmSJEmLaqZ/QJMkSZIkSZIkSZNjauj2TVWVGZaHzOK5bjfN45sNbbdGJNmQZtB6F5ordP/XNJv+DLgO2DrJqAvWbNuuz5/mOA8CvkRzBec9q+rMaY7zk3a93TSP3+A4VbVims/Bimn2n5UkbwL+G/gazSD6lcPbVNUxI46/1VzPaQ2Y+jO0yQzb/GO7nu8g/Bntevd5Po8kSZIkSZK06BzqliRJkiRJkiSpH86muZLxgxbgub7XrncdfqAdmn5ge/O7C3CskZJsBHyZ5nxeNc0VugFor059FnBzRp//w9v1KSOOsxvN4Pi1wB5V9c0Zsr7WrvdMcoOfobQD6A8ArgZmeo55S+PtwCHAyTRX6P7LHJ9u6jXZa8RxtqYZ9r4IuHCOz78632/XO04zkA9w/6Ft5+rd7frgJJvOtGGSm87zWJIkSZIkSdKCcqhbkiRJkiRJkqQeqKorgA8B90ny0lEDskm2SXKnMZ7ueOB3wBOT7DT02CHA1sBXquri+XaPkuTWwFeAnYDDq+olY+z2znb9yiQbDDzXjsDjgV8Dnxo6zp7A54GVwO5V9e2ZDlBVF9AMmm8FPGvo4SOAWwDHVdVVY/TOSZLQDCc/k2YY/dFVdfU8nvI04DzgwUkePXCcdYDXtjePqqqaxzGm1V61/DRgU+BGn+ckdwcOpBm6/+A8j3UacHR7rJOSbDPieOskeTJw7HyOJUmSJEmSJC206a6IIEmSJEmSJEmSJs+zgW2BlwNPSXIGcDlwe2B7YEfgicDPZ3qSqroyyQHAJ4DTknwCuBi4N7An8CvgGWvqJIBPA/cBLgDWSbJsxDbHV9XygdsfBR4D7At8L8nngE1oBrrXBQ6qqj9NbZzkLsAJwAbAF4G9k+w9fJCqGj72M2muCv6WJLvTDETfD3gIcD7w4tmcaJIH0gwtA9yyXW+b5JiBhqcN7PKydvurgeXAC5o57xtYXlXHj3P8qrouyf40V+z+ZJJP0nyud6f5HJwJvGlE9wuAu7Y3d2jX+7fnA3BGVb13nAbg6cDpwOFJHkUz5L2S5irhj6b5edVz2qH6+ToYuI7mNfxxklOBc4FVwObAbsAdaP48SZIkSZIkSRPDoW5JkiRJkiRJknqiqv6UZBfg34EnAfvQDC1fDvwUeB5w8pjPdUKSBwAvAh4GbEQzzH0U8IqqunThz+Bvpq4mvg1w+DTbrKAZagagqirJE2kGrg8AnkMzGHw68MqqOmto/81oXhtoXqd9pjnOssEbVXVBkvvQDM7vBTwCuAx4C3BEVf1uNec27M7AU4fuu83QfU8b+HjqtbkZ8MJpnvNYmqutj6WqvtVe0fwImqH9DYGLaM7xNVW1asRuewG7DN23c7tMGWuou31NdwAOBR5J8wsD6wNXtOfx5hGfvzmpqmuAg5K8j+br5EFt83o0XydnAx+m+cUCSZIkSZIkaWJkDb2bniRJkiRJkiRJkiRJkiRJkiRpDOt0HSBJkiRJkiRJkiRJkiRJkiRJS5lD3ZIkSZIkSZIkSZIkSZIkSZLUIYe6JUmSJEmSJEmSJEmSJEmSJKlDDnVLkiRJkiRJkiRJkiRJkiRJUocc6pYkSZIkSZIkSZIkSZIkSZKkDjnULUmSJEmSJEmSJEmSJEmSJEkdcqhbkiRJkiRJkiRJkiRJkiRJkjrkULckSZIkSZIkSZIkSZIkSZIkdcihbkmSJEmSJEmSJEmSJEmSJEnqkEPdkiRJkiRJkiRJkiRJkiRJktQhh7olSZIkSZIkSZIkSZIkSZIkqUMOdUuSJEmSJEmSJEmSJEmSJElShxzqliRJkiRJkiRJkiRJkiRJkqQOOdQtSZIkSZIkSZIkSZIkSZIkSR1yqFuSJEmSJEmSJEmSJEmSJEmSOuRQtyRJkiRJkiRJkiRJkiRJkiR1yKFuSZIkSZIkSZIkSZIkSZIkSerQ/wOpZp/JGE0mpQAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 2376x1296 with 1 Axes>"
      ]
     },
     "metadata": {
      "image/png": {
       "height": 151,
       "width": 1466
      },
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "time_resolution =  u.hour / 4.0\n",
    "\n",
    "# Create grid of times from ``start_time`` to ``end_time``\n",
    "# with resolution ``time_resolution``\n",
    "time_grid = time_grid_from_range([sunset_start, sunrse_start],\n",
    "                                 time_resolution=time_resolution)\n",
    "\n",
    "constraints = all_constraints\n",
    "observability_grid = np.zeros((len(constraints), len(time_grid)))\n",
    "\n",
    "for i, constraint in enumerate(constraints):\n",
    "    # Evaluate each constraint\n",
    "    observability_grid[i, :] = constraint(het, target, times=time_grid)\n",
    "\n",
    "# Create plot showing observability of the target:\n",
    "\n",
    "extent = [-0.5, -0.5+len(time_grid), -0.5, 3.5]\n",
    "\n",
    "fig, ax = plt.subplots(figsize=(33,18))\n",
    "ax.imshow(observability_grid, extent=extent, origin='lower')\n",
    "\n",
    "ax.set_yticks(range(0, 4))\n",
    "ax.set_yticklabels([c.__class__.__name__ for c in constraints])\n",
    "\n",
    "ax.set_xticks(range(len(time_grid)))\n",
    "ax.set_xticklabels([t.datetime.strftime(\"%H:%M\") for t in time_grid])\n",
    "\n",
    "ax.set_xticks(np.arange(extent[0], extent[1]), minor=True)\n",
    "ax.set_yticks(np.arange(extent[2], extent[3]), minor=True)\n",
    "\n",
    "ax.grid(which='minor', color='w', linestyle='-', linewidth=2)\n",
    "ax.tick_params(axis='x', which='minor', bottom='off')\n",
    "plt.setp(ax.get_xticklabels(), rotation=30, ha='right')\n",
    "\n",
    "ax.tick_params(axis='y', which='minor', left='off')\n",
    "ax.set_xlabel('Time on {0} UTC'.format(time_grid[0].datetime.date()))\n",
    "fig.subplots_adjust(left=0.35, right=0.9, top=0.9, bottom=0.1)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "Nice!  We can visualize the observability for a given night, with all the constraints laid bare.  It looks like Merak is observable just before dawn on the first night of the semester!"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Caveats and expansion\n",
    "\n",
    "- I have not spot-checked that this tool works.  You may want to double check, and I would always recommend using the official online version for any mission-critical applications.  This tool should be considered a first pass or quicklook until it can be vetted further.\n",
    "- In practice, HET tracks have further requirements, such as the ability to acquire a target.  These limitations are not reflected here.\n",
    "- Implementing transit time boundaries in astroplan may be non-trivial.  Check the astroplan documentation or ping me to discuss possible ideas.\n",
    "- There may be a way to speed things up!"
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.7.6"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 2
}