a. Restrict the domain to powers of 2, so $n = 2^{c_1}$ where $c_1$ is some integer greater than or equal
to 1. Our restriction of the domain of $n$ to powers of 2 still permits a conclusive analysis
of $\lceil \lg n \rceil !$ as to how it compares to $c n^k$ as $n$ increases.
We have $\lceil \lg n \rceil ! = \lceil \lg 2^{c_1} \rceil ! = c_1 !$ (by 3.1). By 3.29, this is:
$$
\begin{align}
\sqrt{2 \pi c_1} \left( \frac{c_1}{e} \right)^{c_1} e^{a_n}
\end{align}
$$
where $a_n$ is greater than $1/(12c_1 + 1)$.
The factor $\sqrt{2 \pi c_1}$ is taking the square root of a number greater than 1, so it is greater
than 1. The factor $e^{a_n}$ is taking an increasing root of $e$ as $a_n$ shrinks, but it stays
greater than 1. The factor $\left( c_1 / e \right)^{c_1}$ grows exponentially in $c_1$.
To be polynomially bounded means there is some $cn^k$ that bounds the above expression from above. This
expression is $c (2^{c_1})^k = c (2^k)^{c_1}$. Ignoring the factor of $c$ for a moment, the expression
is a constant taken to the power of $c_1$. Compare the two bases, $2^k$ and $c_1 / e$. Multiply each
by $e$: $c_1$ and $2^k e$.
It is obvious that $c_1 \gt 2^k e$ as $c_1$ grows. It is arbitrarily so. So $(c_1/e)^{c_1}$ is asymtotically
larger than $(2^k)^{c_1}$. So given any constant $c$, there exists an $n_0$ such that
$(c_1 / e)^{c_1} \gt c (2^k)^{c_1}$ for all $n \ge n_0$. So for any constant $k$,
$$
\begin{align}
\lceil \lg n \rceil ! = ω(n^k)
\end{align}
$$
So $\lceil \lg n \rceil !$ is not polynomially bounded.
The ceiling function in this question is, in this part of the exercise, a red herring. We do not examine
its conseqeuences, because the factorial expression beat the polynomial expression without
the help of the ceiling function (it has no effect when its input is an integer, which was the domain
we examined).
For small values of $n$ and $k$, the ceiling function can cause
the two expressions under examination to swap leads as $n$ grows across a window of the domain. But,
regardless of how large $k$ is, $\lceil \lg n \rceil !$ can always catch up to it, and stay ahead,
for all $n$ greater than some $n_0$. Granted, it can take a long time.
Here is a graph for k = 2. The polynomial function is in green, and the factorial function in blue. Over this part
of the early domain, they are competing with each other.
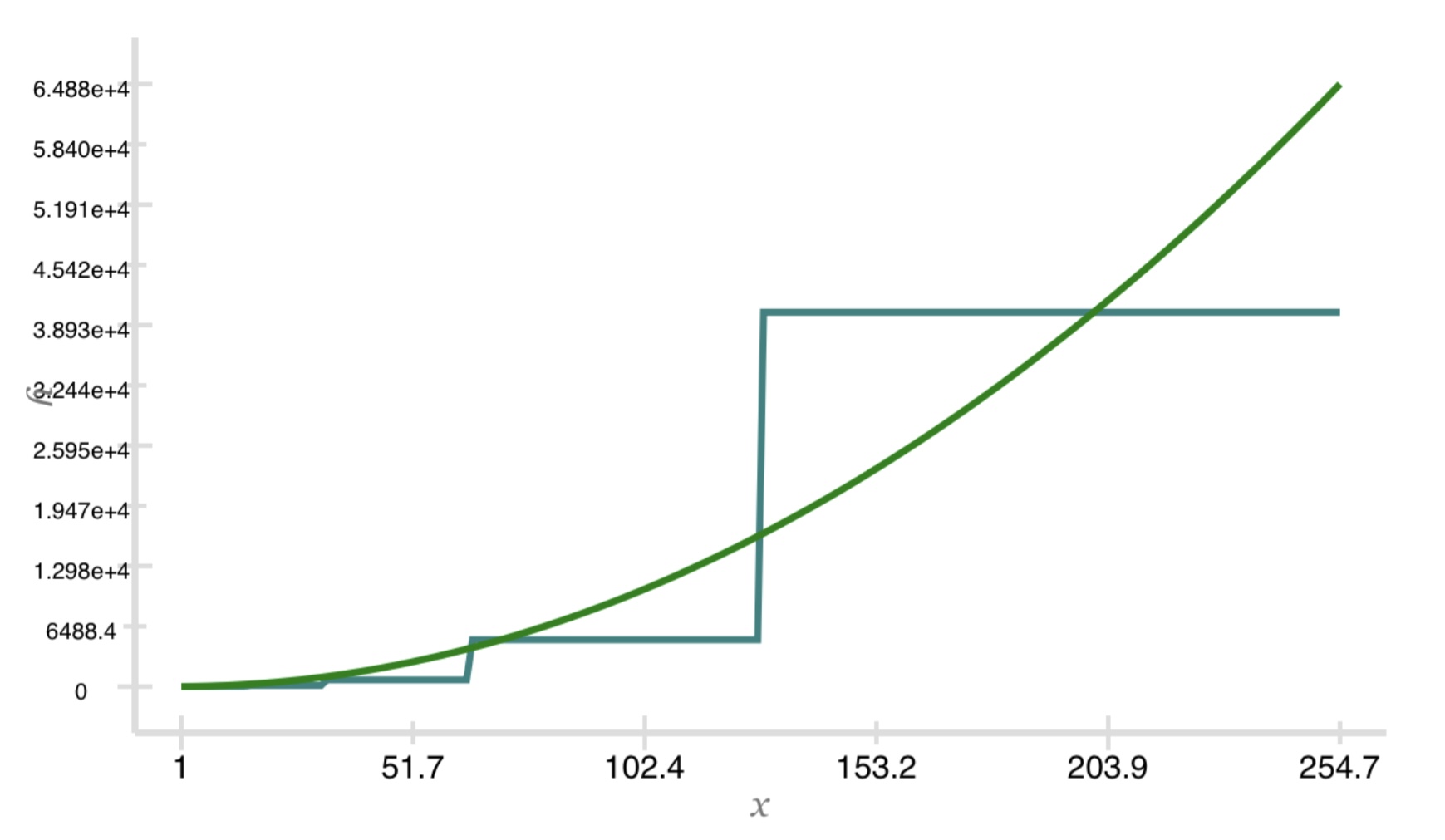
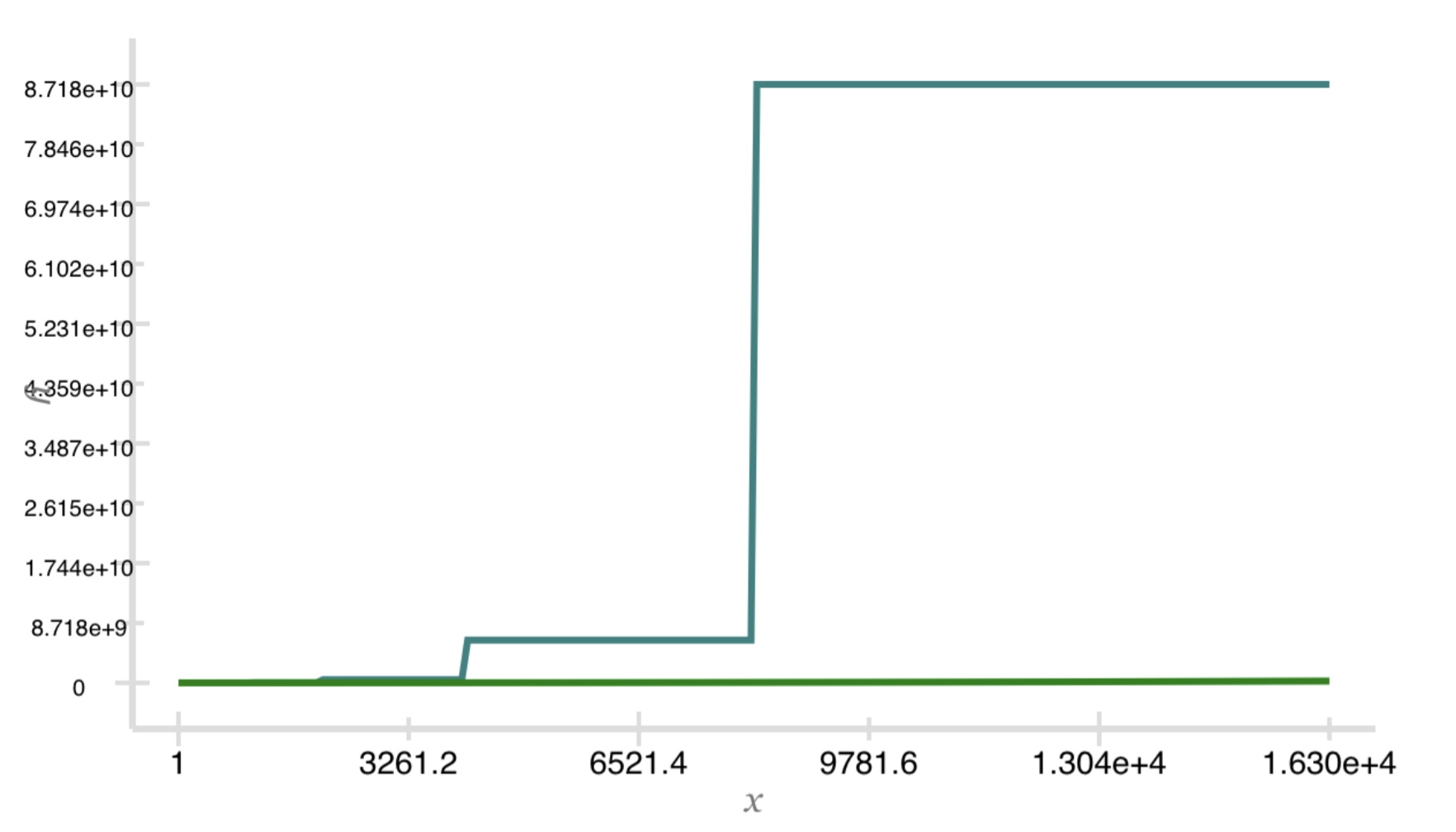
But if we extend the domain from a max of 254 to a max of 1.630e4, the factorial function leaps ahead.
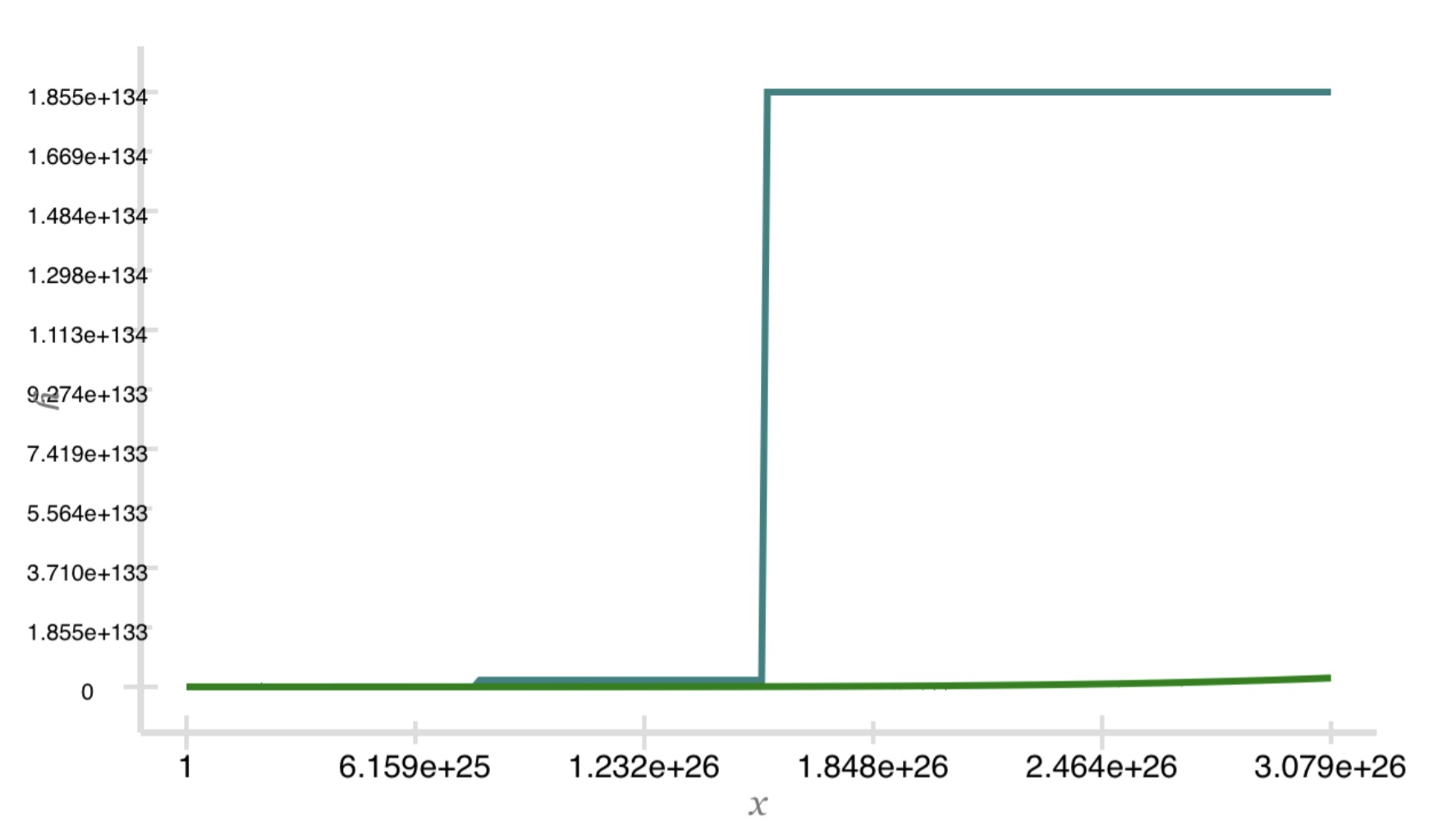
Here is a graph for k = 5. The polynomial function is in green, and the factorial function in blue. The factorial
function in this graph is approximated using 3.29. The exclusive lower bound is used as its value.
b. Similar to part (a), we restrict the domain to values of $n = 2^{c_2}$ where $c_2 = 2^{c_1}$,
$c_1$ is an integer, and $c_1 \ge 1$.
We have $\lceil \lg \lg n \rceil ! = \lceil \lg \lg 2^{c_1} \rceil ! = \lceil \lg c_2 \rceil ! = \lceil c_1 \rceil !$.
By 3.1 again, this is $c_1 !$. By 3.29, similar to part (a), this is:
$$
\begin{align}
\sqrt{2 \pi c_1} \left( \frac{c_1}{e} \right)^{c_1} e^{a_n}
\end{align}
$$
The other expression is:
$$
\begin{align}
n^k &= (2^{c_2})^k \\
&= (2^{2^{c_1}})^k
\end{align}
$$
We take the logarithm base 2 of both expressions. We assume the exclusive upper bound value for $a_n$, so this approximation
is a little too optimistic (it's not going to matter).
$$
\begin{align}
\lg \left( (2 \pi c_1)^{1/2} (\frac{c_1}{e})^{c_1} e^{a_n} \right) &=
\frac{1}{2}\lg 2 \pi c_1 + c_1 (\lg c_1 - \lg e) + a_n \lg e \\
&= \frac{1}{2} \lg 2 \pi + \frac{1}{2} \lg c_1 + c_1 \lg c_1 - c_1 \lg e + \frac{1}{12 c_1} \lg e
\end{align}
$$
When you drop constants and less significant terms, you are left with $c_1 \lg c_1$. $\lg c_1$ doesn't grow
as fast as $c_1$ but let's substitute $c_1$ for it anyway. This gives us ${c_1}^2$.
We turn our attention to the other expression.
$$
\begin{align}
\lg (2^{2^{c_1}})^k &= k \lg 2^{2^{c_1}} \\
&= k 2^{c_1}
\end{align}
$$
Ignoring the coefficient $k$, the two expressions in $c_1$ are $2^{c_1}$ and ${c_1}^2$. We know from
3.13 that any exponential function with a base strictly greater than
1 grows faster than any polynomial function in the same variable. In our case,
this means ${c_1}^2 = o(2^{c_1})$.
We need to address the ceiling function here. It gives the factorial expression a recurring boost relative
to the smooth growth of the polynomial function, $n^k$. To test whether the ceiling function provides
a boost sufficient enough to break the polynomial function, we reevaluate the factorial expression
using $c_2 = 2^{c_1 + 1}$, while leaving the polynomial expression at $2^{c_1}$. This is unfair. Does the polynomial
still win anyway?
We have $\lceil \lg \lg n \rceil ! = \lceil \lg \lg 2^{c_2} \rceil ! = \lceil \lg c_2 \rceil ! = \lceil c_1 + 1 \rceil !
= (c_1 + 1) !$
Using 3.29, this is:
$$
\begin{align}
(c_1 + 1)! &= \left( (2 \pi (c_1 + 1))^{\frac{1}{2}}(\frac{c_1 + 1}{e})^{c_1 + 1} e^{a_n} \right) \\
\end{align}
$$
We take the logarithm base 2 of this to compare it with the polynomial expression.
$$
\begin{align}
&= \frac{1}{2} \lg 2 \pi (c_1 + 1) + (c_1 + 1)\left( \lg (c_1 + 1) - \lg e \right) + \lg e^{a_n} \\
&= \frac{1}{2} \lg 2 \pi + \frac{1}{2} \lg (c_1 + 1) + c_1 \lg (c_1 + 1) - c_1 \lg e + \lg (c_1 + 1) - \lg e + \frac{1}{12(c_1 + 1)} \lg e \\
\end{align}
$$
We eliminate less significant terms.
$$
\begin{align}
&= \frac{1}{2} \lg (c_1 + 1 ) + c_1 \lg (c_1 + 1 ) - c_1 \lg e + \lg (c_1 + 1) + \frac{1}{12(c_1 + 1)} \lg e \\
&= c_1 \lg (c_1 + 1) \\
\end{align}
$$
$\lg (c_1 + 1)$ grows equivalently as fast as $\lg c_1$. Its graph is just shifted to the left. We replace
it with $c_1$, again, to get ${c_1}^2$. As we've already established, this is $o(2^{c_1})$. So the ceiling
function does not provide enough of a boost to the factorial expression to make it keep up with
$n^k$.
So $\lceil \lg \lg n \rceil ! = O(n^k)$. So the function in question
is polynomially bounded. Here is a plot of the two functions. The green is the polynomial function with $k=2$. The aqua
is the factorial function. The graph covers $n$ up to about 3.079e26. The factorial function does not keep up.
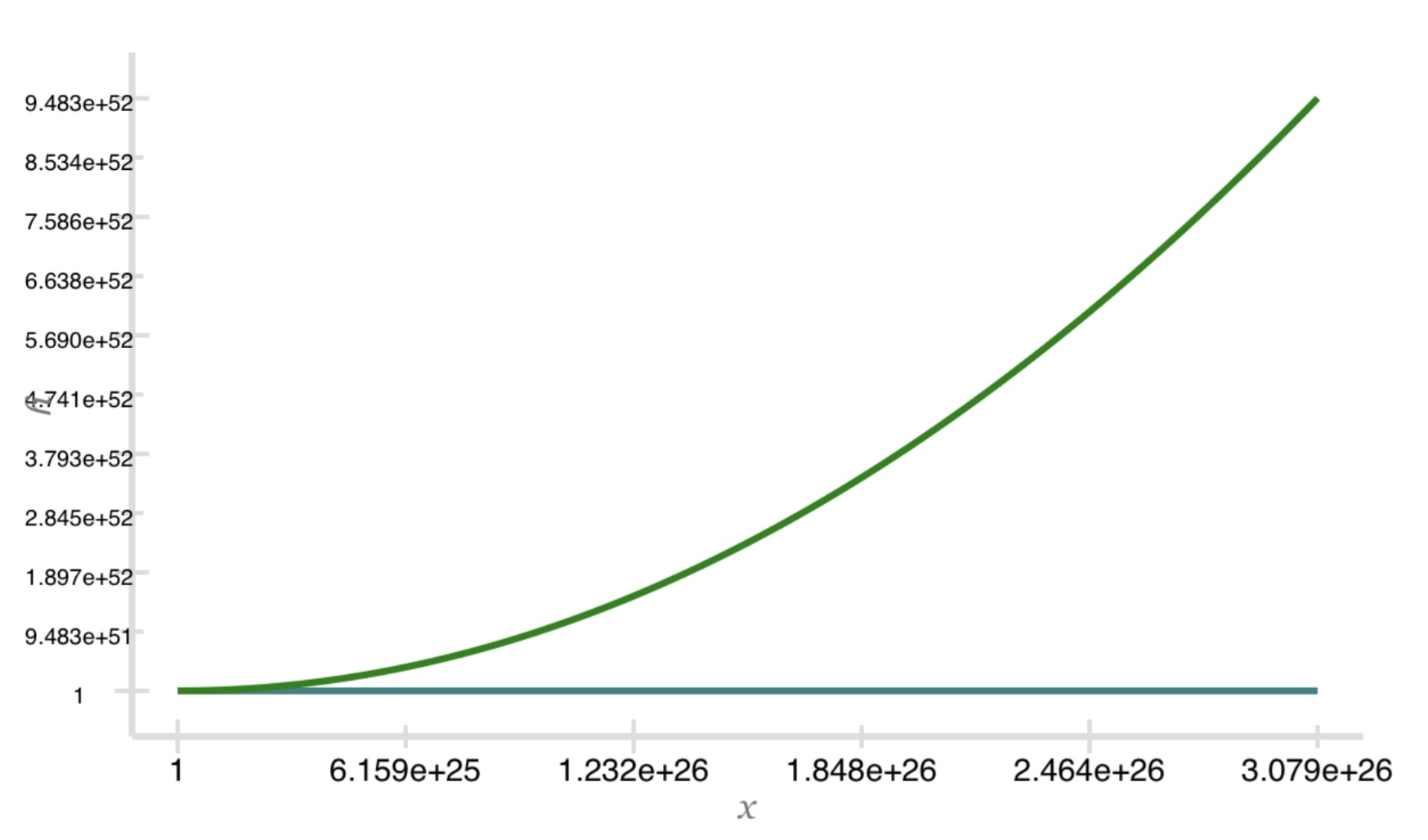
Let's check in with the factorial function at 1.420e45. I used the exclusive upper bound as the value
of the factorial function, from 3.29.
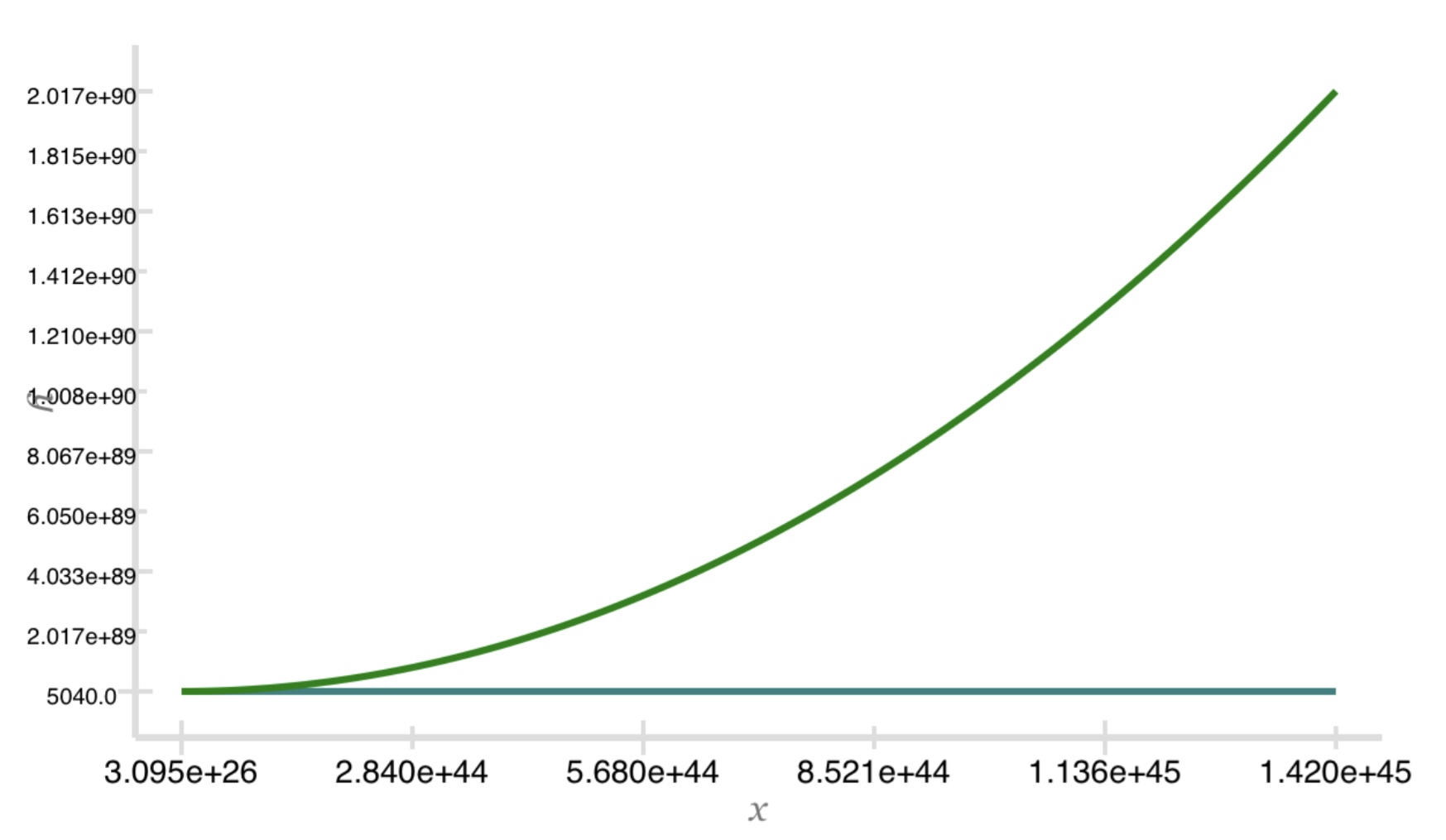
No dice.




