Last active
September 15, 2022 15:25
-
-
Save stackdump/d56ef906cb9a9e55724bb417f4039e13 to your computer and use it in GitHub Desktop.
Finite is a - Rank 1 Constraint System: (R1CS) That uses Petri-Nets as a means to construct Zero Knowledge Proofs.
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| """ | |
| MIT License https://github.com/FactomProject/ptnet-eventstore/blob/master/LICENSE | |
| Finite is a - Rank 1 Constraint System: (R1CS) | |
| That uses Petri-Nets as a means to construct Zero Knowledge Proofs. | |
| The author is planning to deploy using The Factom Blockchain https://www.factom.com/factom-blockchain/ | |
| with the notion that this protocol is useful as an addressing system to index other forms of proofs. | |
| Because Factom can isolate users from the need to own cryptocurrency, it is hoped that adoption can reach outside of | |
| traditional crypto-currency use cases. [ Disclaimer I work for Factom Inc. ] | |
| Symbolic Computation: | |
| --------------------- | |
| Petri-Nets serve as a scaffold for explicitly declaring states of computation using only these operator: [+-*]. | |
| These statemachine/ptnets are translated and applied as: Vector Addition Systems (with state). | |
| https://en.wikipedia.org/wiki/Vector_addition_system | |
| https://en.wikipedia.org/wiki/Petri_net | |
| The input vector delta along with the current an future state are | |
| the inputs data points for the system being recorded and proofed. | |
| Many existing approaches for generic provable computing rely on compiling source code into mathematics. | |
| This approach wields math as a programming language. | |
| Algorithm: | |
| ---------- | |
| The essential aspect of this approach is the use of a linear system solver to calculate a 'witness' vector for | |
| a corresponding secret matrix. A nice feature of this choice is that it ensures exactly one solution exists. | |
| An Inner Product hash of the <public witness>*<solution vector> is used to hide data and produce a unique output. | |
| The inner-product-hash output is converted to a string: by using this yielded decimal value 'x'. | |
| The ouput of: `dot(witness, solution) => x` is then is scaled by 2^n (extracting the mantissa), | |
| and is then base56 encoded (along with adding a prefix to denote negative or positive values. | |
| This base56 encoded string taken along with the corresponding | |
| public witness vector serve as a globally unique hashid that encodes a state-machine transation. | |
| Safety: | |
| ------- | |
| Because we only expose a mathematical fingerprint from our hidden state machine, | |
| it should be very difficult or impossible to guess the protected internal state. (#REVIEW more thought needed here) | |
| To forge an event-proof, a user must know or guess the state or transition vector, | |
| along with the other n-1 random vectors needed to compose the hash. Addtionally, | |
| because we are using a universal hash family as our algorithm this is thought to | |
| be very difficult or impossible to reverse engineer from the output fingerprint. | |
| If the security of this approach is faulty and it allows for successful forgery of a given event, | |
| each value can still be measured for correctness against adjacent events (presumably on a blockchain) | |
| to audit for continuity. | |
| Extensibility: | |
| -------------- | |
| It's notable that only 1/n rows of our secret matrix contain data. | |
| The others are randomly generated values to pad out/construct a square matrix. | |
| These added random vectors can be though of as a type of One-Time-Pad OTP. | |
| This offers protection against statistical attacks, however if we were to re-use | |
| the same hash for every interaction it may be possible to guess the cleartext. | |
| Because the actual hash algorithm is specified at runtime via the witness vector, | |
| we are able to intermingle useful data or identifiers as part of a challenge-response interaction. | |
| Also NOTE: any of the randomly generated vectors in the padded data can be substituted | |
| for meaningful information. Using this feature, it's possible to create multiple fingerprints | |
| of the same data or to correlate identifiers between 2 isolated systems. | |
| Application: | |
| ------------ | |
| The purpose of a ledger (distributed or not) is to collect and aggregate groups of numbers. | |
| This very approach is made useful for general purpose algorithms thanks to the application of | |
| this state-vector style of state machine. | |
| Conclusion: | |
| ----------- | |
| We also avoid the difficulty from previous approaches that sought use a compiler to | |
| convert source code to mathematics whereas this approach seeks to minimize the calculations being witnessed. | |
| By adopting a mathematically rigorous toolkit to build higher-level program logic we can | |
| build very complex processes that can be made "proof-able" without having to deviate from a core protocol. | |
| """ | |
| from baseconv import base56 | |
| from numpy import dot, cross, array, linalg, allclose, frexp | |
| from numpy.random import randint, seed | |
| class Finite(object): | |
| """ prefix for positive numbers """ | |
| POS = '45' | |
| """ prefix for negative numbers """ | |
| NEG = '83' | |
| @staticmethod | |
| def encode(n): | |
| """ encode float to user string """ | |
| return base56.encode( | |
| ("%.54f" % n).replace('-0.', Finite.NEG).replace('0.', Finite.POS) | |
| ) | |
| @staticmethod | |
| def decode(s): | |
| """ decode float value from user string """ | |
| h = base56.decode(s) | |
| sign = '' | |
| if h[1] == Finite.NEG[1]: | |
| sign = '-' | |
| assert h[0] == Finite.NEG[0] | |
| else: | |
| assert h[0] == Finite.POS[0] | |
| assert h[1] == Finite.POS[1] | |
| return float(sign+'0.'+h[2:]) | |
| @staticmethod | |
| def scale(x): | |
| """ | |
| this scales the result by the smallest possible exponent 2**exp | |
| https://docs.scipy.org/doc/numpy/reference/generated/numpy.frexp.html | |
| Decompose the elements of x into mantissa and twos exponent. | |
| Returns (mantissa, exponent), where x = mantissa * 2**exponent`. | |
| The mantissa is lies in the open interval(-1, 1), | |
| while the twos exponent is a signed integer. | |
| """ | |
| h, _ = array(frexp(x)).tolist() | |
| # ^ NOTE: that we throw away the exp value | |
| # this guarentees that the secret data cannot | |
| # be reverse engineered via brute force | |
| return h | |
| @staticmethod | |
| def rand_num(capacity=1e6): | |
| return int(capacity/2 - randint(1, capacity)) | |
| # generate a vector of random integers | |
| @staticmethod | |
| def rand_vector(capacity): | |
| out = [] | |
| i = 0 | |
| for _ in capacity: | |
| out.append(Finite.rand_num()) | |
| return out | |
| @staticmethod | |
| def vector(capacity, default_scalar): | |
| out = [] | |
| for _ in capacity: | |
| out.append(default_scalar) | |
| return out | |
| @staticmethod | |
| def proof(capacity, data, nonce, witness=None): | |
| """ | |
| generates a random proof used to demonstrate | |
| that we know a matrix 'm' where: | |
| m[0] vector contains our target data | |
| and: dot(m, soln) = witness | |
| """ | |
| seed(nonce) | |
| k = len(data) | |
| if k < 3: | |
| raise Exception('state must have at least 3 places') | |
| allzeros = True | |
| for s in data: | |
| if s != 0: | |
| allzeros = False | |
| if allzeros: | |
| raise Exception('secret data must not be all zeros') | |
| m = [data] # add target data | |
| # append random vectors to make it square | |
| while len(m) < k: | |
| m.append(Finite.rand_vector(capacity)) | |
| if not witness: | |
| witness = Finite.rand_vector(capacity) | |
| soln = None | |
| try: | |
| # solve the system for a private solution to secret + witness | |
| soln = linalg.solve(m, witness) | |
| assert allclose(dot(m, soln), witness) # assert math works | |
| except linalg.LinAlgError as err: | |
| # since our matrix is randomly generated there is no guarenteed a solution exists | |
| # rotate the nonce and try again | |
| return proof(capacity, data, randint(1,1e6), witness=witness) | |
| return nonce, m, witness, soln, Finite.scale(dot(witness, soln)) | |
| class AuctionContract(object): | |
| """ | |
| Execute an auction contract building upon | |
| state machine ruleset | |
| Program states are used to construct Zero-Knowledge Proofs for the given event stream. | |
| """ | |
| places = [ | |
| "PRICE", | |
| "NEW", | |
| "OPEN", | |
| "ACCEPTED", | |
| "REJECTED", | |
| ] | |
| # initial state for the places labeled above | |
| state = array([0, 1, 0, 0, 0]) | |
| # set place value limits | |
| capacity = [10000, 1, 1, 1, 1] # NOTE price field has a max of 10k | |
| transitions = { | |
| "EXEC": [0,-1,1,0,0], | |
| "SOLD": [0,0,-1,1,0], | |
| "HALT": [0,0,-1,0,1], | |
| "BID": [1,0,0,0,0], | |
| } | |
| # guards and conditions contain transition vectors for | |
| # inspecting/testing the state of the system | |
| # these serve as conditional tools | |
| # or in petri-net terms these are called 'inhibitor arcs' | |
| # see also: Dual Petri-Nets or Fuzzy Nets | |
| guards = [] # inhibit action based on identity | |
| conditions = [] # inhibit redemption based on state | |
| # trigger state machine transformation | |
| # and construct corresponding proofs | |
| def commit(self, delta, nonce): | |
| output = array(self.state) + delta | |
| i = 0 | |
| # enforce state machine rules | |
| while i < len(output): | |
| assert output[i] >= 0 # state allows uint only | |
| assert output[i] <= AuctionContract.capacity[i] | |
| i += 1 | |
| # create input proof | |
| n0, m0, w0, s0, h0 = Finite.proof(self.capacity, self.state, nonce) | |
| # transform state | |
| self.state = output | |
| # create output proof | |
| n1, m1, w1, s1, h1 = Finite.proof(self.capacity, self.state, nonce) | |
| return { | |
| "priv": { | |
| "input": { | |
| "nonce": n0, | |
| "data": m0[0].tolist(), | |
| "witness": s0.tolist() | |
| }, | |
| "output": { | |
| "nonce": n1, | |
| "data": m1[0].tolist(), | |
| "witness": s1.tolist() | |
| }, | |
| }, | |
| "pub": { | |
| "witness": w0, | |
| "input": Finite.encode(h0), | |
| "ouput": Finite.encode(h1) | |
| } | |
| } | |
| # generate a sequence of events with accompanying proofs | |
| if __name__ == '__main__': | |
| m = AuctionContract() | |
| def action(label, mult=1): | |
| nonce = randint(1,1e6) | |
| soln = m.commit(array(m.transitions[label])*mult, nonce) | |
| print('==========') | |
| print(' %s => %s' % (label, soln['priv']['output']['data'])) | |
| print('----------') | |
| print(' private:\n input: %s\n output: %s' % (soln['priv']['input'], soln['priv']['output'])) | |
| print('----------') | |
| print(' public: %s' % soln['pub']) | |
| action('EXEC') | |
| action('BID', mult=123) | |
| action('SOLD') |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| ========== | |
| EXEC => [0, 0, 1, 0, 0] | |
| ---------- | |
| private: | |
| input: {'nonce': 798933, 'data': [0, 1, 0, 0, 0], 'witness': [294838.7162005816, 200019.99999999994, -204496.34792476898, -366889.7632200806, -497189.0879542028]} | |
| output: {'nonce': 798933, 'data': [0, 0, 1, 0, 0], 'witness': [-288390.6725547537, -195638.199531369, 200019.99999999994, 358874.50410049077, 486313.87333379756]} | |
| ---------- | |
| public: {'witness': [200020, -147004, 414188, -333807, -141101], 'input': 'X8gskgzDFtBgz7aAmZqFFvYitYNCgTiC', 'ouput': 'xjivERMJJzTmH9mAsa4XBZmExfCmM9YW'} | |
| ========== | |
| BID => [123, 0, 1, 0, 0] | |
| ---------- | |
| private: | |
| input: {'nonce': 454076, 'data': [0, 0, 1, 0, 0], 'witness': [2220140.4765694416, 69854.1761815485, 493146.99999999994, -1845234.2059134028, -592862.4298040231]} | |
| output: {'nonce': 454076, 'data': [123, 0, 1, 0, 0], 'witness': [4002.0940952935302, 126.05021754519018, 889.4262788957474, -3326.5992578905184, -1068.0196395516398]} | |
| ---------- | |
| public: {'witness': [493147, 235233, -173565, 15223, -218558], 'input': 'X99iGqduZWrL4UkqudQ8iHtuZVJTaqHW', 'ouput': 'XQfjVA5UTMTwkMwZMMH5fr4fNnzEhiWY'} | |
| ========== | |
| SOLD => [123, 0, 0, 1, 0] | |
| ---------- | |
| private: | |
| input: {'nonce': 114746, 'data': [123, 0, 1, 0, 0], 'witness': [3046.262180108822, 1737.3193113698476, -325.248153385134, 2097.462174976482, 1336.1617062360576]} | |
| output: {'nonce': 114746, 'data': [123, 0, 0, 1, 0], 'witness': [3026.6750325135613, 1726.1351630260967, -323.16203032250644, 2083.9710008318716, 1327.5567412804123]} | |
| ---------- | |
| public: {'witness': [374365, -222092, 244549, -44439, -35165], 'input': 'XSUMup6yPgxzafubB2mypbNZpQsQxgNQ', 'ouput': 'XSFWUqF5ApfBrUAk9y3CVdJcze63MPbs'} |
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
One other interesting thought about using a finite-state machine to define a process is that the resulting labels of the system
form a regular language:
Kleene's theorem
Some of my previous thoughts about Petri-Nets can be found here https://www.blahchain.com/posts/ubiquitous_langage_with_PNML.html
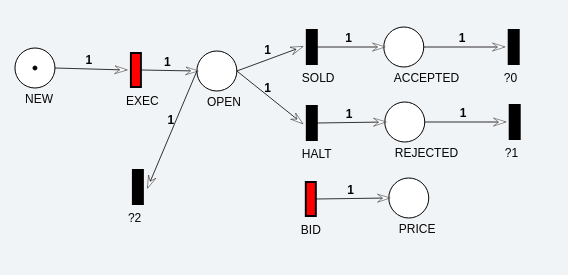
This figure shows a graphical petri-net that matches the rules from the example code above. (NOTE: it also has some transitions marked with '?' which are meant to be eventually used via guards & roles)
Learn More about the Factom Blockchain https://www.factom.com/factom-blockchain/